Postać kanoniczna funkcji kwadratowej
Postać kanoniczna funkcji kwadratowej (trójmianu kwadratowego) wyrażonej w postaci ogólnej \(y=ax^2+bx+c\) jest następująca:
gdzie
jest to tak zwany wyróżnik trójmianu kwadratowego, potocznie nazywany „deltą”.
Wzór na deltę
Powyższy wzór na deltę to jeden z najważniejszych wzorów w matematyce, który pojawia się bardzo często w zagadnieniach matematycznych, przy rozwiązywaniu zadań. W przypadku funkcji kwadratowej przydaje się na przykład przy rozwiązywaniu równań i nierówności kwadratowych.
Postać kanoniczna funkcji kwadratowej jest wygodna, gdy musimy sporządzić wykres funkcji kwadratowej lub określić jej własności (monotoniczność, ekstremum funkcji itp.). Korzystamy tutaj przy tym z przesunięcia wykresu funkcji \(y=ax^2\) o wektor \(\vec{u}=[-\frac{b}{2a},-\frac{\Delta}{4a}]\).
Zamiana postaci ogólnej funkcji kwadratowej na kanoniczną
Zamiana postaci ogólnej funkcji kwadratowej na kanoniczną sprowadza się do podstawienia do wzoru na postać kanoniczną odpowiednich współczynników.
Przykłady
Sprowadzimy do postaci kanonicznej funkcję \(f(x)=2x^2-4x+12\).
Mamy tutaj:
\(a=2, b=-4, c=12\)
Obliczamy wyróżnik trójmianu kwadratowego:
\(\Delta=b^2-4ac=(-4)^2-4\cdot{2}\cdot{12}=16-96=-80\)
Wstawiamy więc liczby do wzoru:
\(y=a(x+\frac{b}{2a})^2-\frac{\Delta}{4a}=2(x+\frac{-4}{4})^2-\frac{-80}{8}=2(x-1)^2+10\)
Zamiana postaci kanonicznej funkcji kwadratowej na postać ogólną
W tym przypadku należy wykonać potęgowanie z użyciem wzorów skróconego mnożenia i uporządkować wyrazy.
Sprowadzimy do postaci ogólnej funkcję \(f(x)=2(x-1)^2+3\).
Wykonujemy działania:
\(f(x)=2(x-1)^2+3=2(x^2-2x+1)+3=2x^2-4x+5\)
Wyprowadzenie postaci kanonicznej trójmianu kwadratowego
Poniżej wyprowadzamy postać kanoniczną trójmianu kwadratowego.
\(y=ax^2+bx+c\).
Z definicji trójmianu kwadratowego wynika, że \(a\neq 0\) więc możemy wyjąć ten współczynnik przed nawias.
\(y=a(x^2+\frac{b}{a}x+\frac{c}{a})\)
Należy się pozbyć potęgi przy \(x\). Możemy skorzystać ze wzoru skróconego mnożenia:
\(x^2+2A+A^2=(x+A)^2\),
przy czym nie mamy jeszcze takiej postaci w naszym wzorze. \(A\) oznacza pewne wyrażenie liczbowe, musimy jednak najpierw uzyskać wyraz \(2A\).
\(y=a(x^2+2\cdot \frac{b}{2a}x+\frac{c}{a})\)
Mamy więc już wyraz \(2A=2\frac{b}{2a}\), więc \(A=\frac{b}{2a}\). Brakuje nam jeszcze wyrazu \(A^2\), czyli \(A^2=(\frac{b}{2a})^2\). Możemy go dodać do naszego wzoru, ale aby otrzymać zdanie prawdziwe musimy je także odjąć:
\(y=a[x^2+2\cdot \frac{b}{2a}x+(\frac{b}{2a})^2-(\frac{b}{2a})^2 + \frac{c}{a}]\)
Dla podkreślonych wyrazów możemy więc zastosować wspomniany wyżej wzór skróconego mnożenia.
\(y=a[\underline{x^2+2\cdot \frac{b}{2a}x+(\frac{b}{2a})^2}-(\frac{b}{2a})^2+\frac{c}{a}]\)
Otrzymujemy zatem:
\(y=a[(x+\frac{b}{2a})^2-(\frac{b}{2a})^2+\frac{c}{a}]\)
Teraz obliczamy wyraz wolny i mnożymy wyrazy w nawiasie przez \(a\).
\(y=a[(x+\frac{b}{2a})^2-\frac{b^2}{4a^2}+\frac{4ac}{a^2}]\)
\({y=a[(x+\frac{b}{2a})^2-\frac{b^2-4ac}{4a^2}]}\)
\({y=a(x+\frac{b}{2a})^2-a\cdot \frac{b^2-4ac}{4a^2}}\)
\({y=a(x+\frac{b}{2a})^2-\frac{b^2-4ac}{4a}}\)
Wprowadzając oznaczenie \(\Delta=b^2-4ac\), otrzymujemy postać kanoniczną:
\(y=a(x+\frac{b}{2a})^2-\frac{\Delta}{4a}\)
Zadania z rozwiązaniami

Zadanie nr 1.
Sprowadzić do postaci kanonicznej funkcję \(f(x)=2x^2+2x+1\).

Zadanie nr 2.
Wykres funkcji \(y=-x^2\) przesunięto o wektor \(\vec{u}=[-5,5]\). Jakie jest równanie paraboli, powstałej w wyniku przesunięcia?

Zadanie nr 3 — maturalne.
Wykresem funkcji kwadratowej \(f(x)=3x^2+bx+c\) jest parabola o wierzchołku w punkcie \(W=(−3,2)\). Wzór tej funkcji w postaci kanonicznej to
A. \(f(x)=3(x-3)^2+2\)
B. \(f(x)=3(x+3)^2+2\)
C. \(f(x)=(x-3)^2+2\)
D. \(f(x)=(x+3)^2+2\)
Powiązane materiały
© medianauka.pl, 2009-07-19, A-268
Data aktualizacji artykułu: 2023-04-18

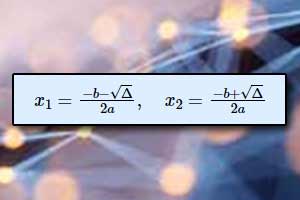 Miejsca zerowe funkcji kwadratowej
Miejsca zerowe funkcji kwadratowej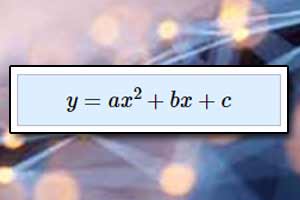 Funkcja kwadratowa
Funkcja kwadratowa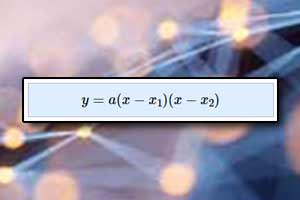 Postać iloczynowa trójmianu kwadratowego
Postać iloczynowa trójmianu kwadratowego Parabola
Parabola Właściwości i wykres funkcji kwadratowej
Właściwości i wykres funkcji kwadratowej