Przesunięcie wykresu funkcji
Jeżeli punkt \(A\) o współrzędnych \((x,y)\) przesuniemy w układzie współrzędnych o wektor \(\vec{v}=[p,q]\), to otrzymamy punkt \(A'\) o współrzędnych \((x+p,x+q)\).
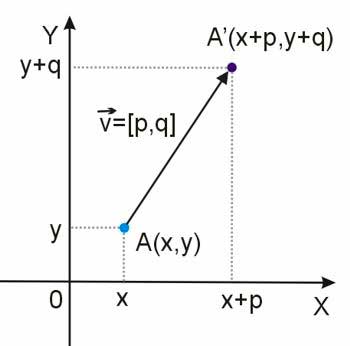
Ponieważ wykres funkcji (oznaczmy go literą \(W\)) jest figurą geometryczną, więc przesunięcie całego wykresu polega na przesunięciu wszystkich punktów wykresu o ten sam wektor przesunięcia.
Wiemy, że każdy punkt wykresu \(W\) spełnia zależność \(y=f(x)\). Jaki będzie zatem wzór funkcji wykresu \(W'\) powstałego z przesunięcia wykresu \(W\) o wektor \(\vec{v}=[p,q]\)?
Przesunięcie wykresu funkcji o wektor
Jeżeli współrzędne punktów należących do wykresu \(W'\) mają postać \((x,y)\), to współrzędne punktów wykresu W są postaci \((x-p, y-q)\). Podstawiamy więc współrzędne do wzoru funkcji i otrzymujemy: \(y-q=f(x-p)\).
Otrzymaliśmy w ten sposób wykres funkcji \(y=f(x)\) przesunięty w układzie współrzędnych o wektor \(\vec{v}=[p,q]\).
Przykład
Naszkicujmy wykres funkcji \(y=x^2-2x+3\), korzystając z informacji zawartych wyżej.
Aby to uczynić, musimy przekształcić nieco wzór funkcji (doprowadzić do właściwej postaci):
\(y=(x^2-2x+1)+2\)
\(y=(x-1)^2+2\)
Zatem musimy przesunąć wykres funkcji \(y=x^2\) o wektor \(\vec{v}=[1,2]\).
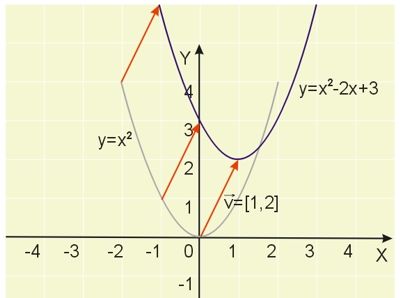
Przesuwanie wykresów funkcji w układzie współrzędnych ma duże znaczenie praktyczne. Możemy szybko naszkicować wiele wykresów funkcji, znając jedynie wykresy funkcji elementarnych i powyższą zasadę znajdowania wektora przesunięcia. Poniżej jeszcze kilka przykładów stosowania tej zasady.
Przykłady
- Aby naszkicować wykres funkcji \(y=\frac{1}{x+12}+7\), wystarczy wykres funkcji \(y=\frac{1}{x}\) przesunąć o wektor \(\vec{v}=[-12,7]\).
- Aby naszkicować wykres funkcji \(y=-1+\log{(x-8)}\), wystarczy wykres funkcji \(y=\log{x}\) przesunąć o wektor \(\vec{v}=[8,-1]\).
- Aby naszkicować wykres funkcji \(y=\cos{(x+\frac{\pi}{6})}\), wystarczy wykres funkcji \(y=\cos{x}\) przesunąć o wektor \(\vec{v}=[\frac{\pi}{6},0]\).
- Aby naszkicować wykres funkcji \(y=\sqrt{x+5}-5\), wystarczy wykres funkcji \(y=\sqrt{x}\) przesunąć o wektor \(\vec{v}=[-5,-5]\).
Warto poćwiczyć przesuwanie wykresu funkcji na niżej opublikowanych zadaniach.
Przesunięcie wykresu funkcji wzdłuż osi OX
Otrzymaliśmy w ten sposób wykres funkcji \(y=f(x)\) przesunięty w układzie współrzędnych o wektor \(\vec{v}=[p,0]\).
Przesunięcie wykresu funkcji wzdłuż osi OY
Otrzymaliśmy w ten sposób wykres funkcji \(y=f(x)\) przesunięty w układzie współrzędnych o wektor \(\vec{v}=[0,q]\).
Przesunięcie wykresu funkcji kwadratowej
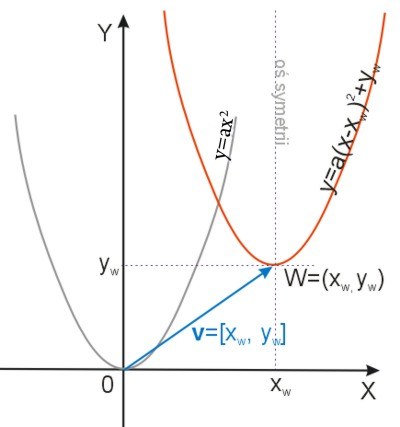
Wykres funkcji: \(y=ax^2+bx+c=a(x+\frac{b}{2a})^2-\frac{\Delta}{4a}=a(x-x_w)^2+y_w\) jest parabolą, która powstaje w wyniku przesunięcia wykresu funkcji \(y=ax^2\) o wektor \(\vec{v}=[x_w,y_w]\), przy czym \(x_w=-\frac{b}{2a},\quad{y_w}=-\frac{\Delta}{4a}\)
W przypadku dodatniego współczynnika \(a\) mamy:
Zadania z rozwiązaniami

Zadanie nr 3.
Naszkicować wykres funkcji \(y=\log_{\frac{1}{3}}{(x-3)}+1\).

Zadanie nr 5.
Naszkicować wykres funkcji \(y=\log_{\frac{1}{2}}{(\sqrt{2}x+2\sqrt{2})}+1\).

Zadanie nr 9 — maturalne.
Na rysunku przedstawiono fragment wykresu funkcji \(f\), który powstał w wyniku przesunięcia wykresu funkcji określonej wzorem \(y=\frac{1}{x}\) dla każdej liczby rzeczywistej \(x\neq 0\).
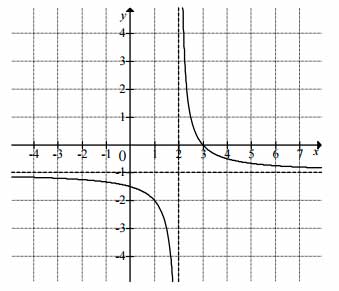
a) Odczytaj z wykresu i zapisz zbiór tych wszystkich argumentów, dla których wartości funkcji \(f\) są większe od \(0\).
b) Podaj miejsce zerowe funkcji \(g\) określonej wzorem \(g(x)=f(x-3)\).

Zadanie nr 10 — maturalne.
Na poniższym rysunku przedstawiono wykres funkcji \(f\) określonej w zbiorze \([−6, 5]\).
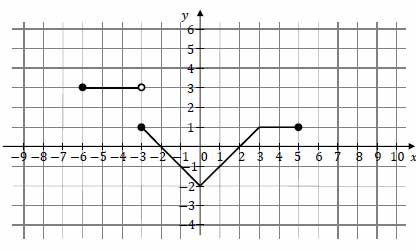
Funkcja \(g\) jest określona wzorem \(g(x)=f(x)-2\) dla \(x\in [−6, 5]\). Wskaż zdanie prawdziwe.
A. Liczba \(f(2)+g(2)\) jest równa \((−2)\).
B. Zbiory wartości funkcji \(f\) i \(g\) są równe.
C. Funkcje \(f\) i \(g\) mają te same miejsca zerowe.
D. Punkt \(P=(0,−2)\) należy do wykresów funkcji \(f\) i \(g\).

Zadanie nr 11 — maturalne.
Na rysunku 1. przedstawiono wykres funkcji \(f\) określonej na zbiorze \(\langle -4; 5\rangle\).
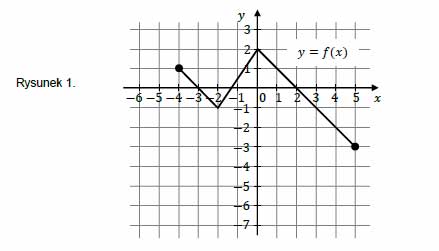
Funkcję \(g\) określono za pomocą funkcji \(f\). Wykres funkcji \(g\) przedstawiono na rysunku 2.
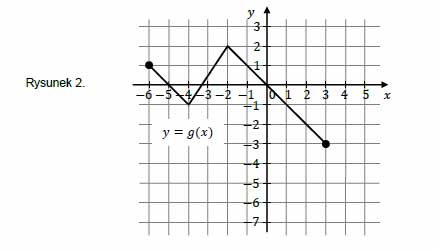
Wynika stąd, że
A. \(g(x)=f(x)-2\)
B. \(g(x)=f(x-2)\)
C. \(g(x)=f(x)+2\)
D. \(g(x)=f(x+2)\)
Powiązane materiały
© medianauka.pl, 2009-05-24, A-216
Data aktualizacji artykułu: 2023-04-08

 Układ współrzędnych
Układ współrzędnych Wykres funkcji z wartością bezwzględną
Wykres funkcji z wartością bezwzględną Wykres funkcji
Wykres funkcji Pomocniczy układ współrzędnych
Pomocniczy układ współrzędnych Wykres funkcji jednej zmiennej
Wykres funkcji jednej zmiennej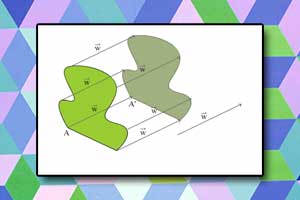 Translacja
Translacja