Zadanie - szkicowanie wykresu funkcji logarytmicznej
Treść zadania:
Naszkicować wykres funkcji \(y=\log_{\frac{1}{2}}{(\sqrt{2}x+2\sqrt{2})}+1\).
Rozwiązanie zadania
Wyrażenie pod logarytmem nie jest proste. Sporządzanie tabelki zmienności funkcji nie jest więc tutaj takie proste. W tym przypadku można sobie ułatwić pracę związaną ze sporządzaniem wykresu tej funkcji, gdyż można tu skorzystać z możliwości s przesuwania wykresu funkcji w układzie współrzędnych o dany wektor. Przypomnijmy:
Funkcja \(y=f(x)\) przesunięta w układzie współrzędnych o wektor \(\vec{u}=[p,q]\) ma postać \(y-q=f(x-p)\).
Musimy zatem wzór danej funkcji przekształcić do żądanej postaci. Po przeniesieniu jedności na drugą stronę równości należy wyjąć pierwiastek z dwóch przed nawias pod logarytmem:
\(y=\log_{\frac{1}{2}}{(\sqrt{2}x+2\sqrt{2})}+1\)
\(y-1=\log_{\frac{1}{2}}{[\sqrt{2}(x+2)]}\)
Następnie należy skorzystać z własności działań na logarytmach:
\(\log_{a}{b\cdot c}=\log_{a}{b}+\log_{a}{c}\)Powyższy wzór jest prawdziwy dla \(a, b\) i \(c\) dodatnich i podstawa logarytmu musi być różna od jedności. Zgodnie z nim (w pierwszym kroku przekształceń) mamy:
\(y-1=\log_{\frac{1}{2}}{[\sqrt{2}\cdot (x+2)]}\)
\(y-1=\log_{\frac{1}{2}}{\sqrt{2}} + \log_{\frac{1}{2}}{(x+2)}\)
\(y-1=-\frac{1}{2} + \log_{\frac{1}{2}}{(x+2)}\)
\(y-1+\frac{1}{2}=\log_{\frac{1}{2}}{(x+2)}\)
\( y-\frac{1}{2}=\log_{\frac{1}{2}}{[x-(-2)]}\)
\( y-q=f(x-p)\)
Na niebiesko zaznaczono fragment obliczeń: \(\log_{\frac{1}{2}}{\sqrt{2}}=-\frac{1}{2}\), bo \((\frac{1}{2})^{-\frac{1}{2}}=2^{\frac{1}{2}}=\sqrt{2}\)
Aby wykonać wykres naszej funkcji wystarczy więc wykres funkcji \(y=\log_{\frac{1}{2}}{x}\) przesunąć o wektor \(\vec{u}=[p,q]=[-2,\frac{1}{2}]"\).
Sporządzamy tabelkę zmienności funkcji elementarnej, a potem wykres:
\(x\)\(\frac{1}{4}\)\(\frac{1}{2}\)\(1\)\(2\)\(4\)\(y=\log_{\frac{1}{2}}{x}\)\(2\)\(1\)\(0\)\(-1\)\(-2\)© medianauka.pl, 2009-12-09, ZAD-421


Zadania podobne
Zadanie nr 3.
Naszkicować wykres funkcji \(y=\log_{\frac{1}{3}}{(x-3)}+1\).

Zadanie nr 8 — maturalne.
Na rysunku przedstawiono fragment wykresu funkcji \(f\), który powstał w wyniku przesunięcia wykresu funkcji określonej wzorem \(y=\frac{1}{x}\) dla każdej liczby rzeczywistej \(x\neq 0\).
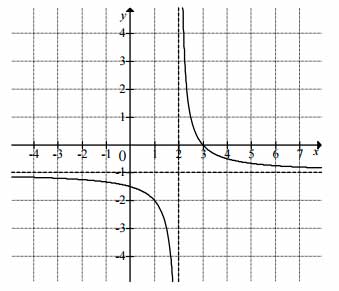
a) Odczytaj z wykresu i zapisz zbiór tych wszystkich argumentów, dla których wartości funkcji \(f\) są większe od \(0\).
b) Podaj miejsce zerowe funkcji \(g\) określonej wzorem \(g(x)=f(x-3)\).

Zadanie nr 9 — maturalne.
Na poniższym rysunku przedstawiono wykres funkcji \(f\) określonej w zbiorze \([−6, 5]\).
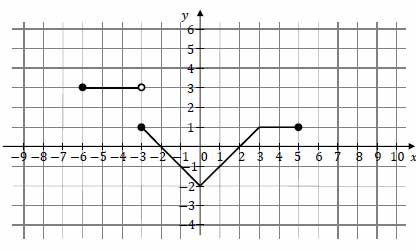
Funkcja \(g\) jest określona wzorem \(g(x)=f(x)-2\) dla \(x\in [−6, 5]\). Wskaż zdanie prawdziwe.
A. Liczba \(f(2)+g(2)\) jest równa \((−2)\).
B. Zbiory wartości funkcji \(f\) i \(g\) są równe.
C. Funkcje \(f\) i \(g\) mają te same miejsca zerowe.
D. Punkt \(P=(0,−2)\) należy do wykresów funkcji \(f\) i \(g\).

Zadanie nr 10 — maturalne.
Na rysunku 1. przedstawiono wykres funkcji \(f\) określonej na zbiorze \(\langle -4; 5\rangle\).
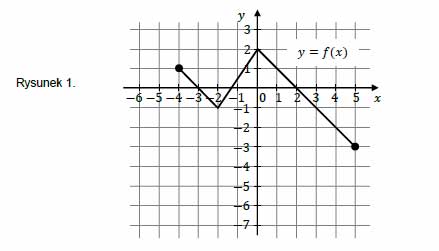
Funkcję \(g\) określono za pomocą funkcji \(f\). Wykres funkcji \(g\) przedstawiono na rysunku 2.
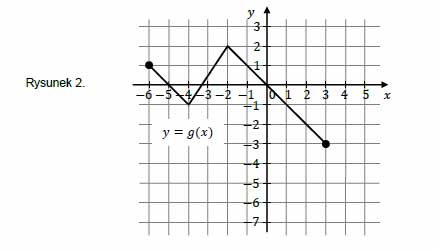
Wynika stąd, że
A. \(g(x)=f(x)-2\)
B. \(g(x)=f(x-2)\)
C. \(g(x)=f(x)+2\)
D. \(g(x)=f(x+2)\)

