Zadanie - Wykres funkcji homograficznej y=(-4x+7)/(2x-2)
Treść zadania:
Sporządzić wykres funkcji \(y=\frac{-4x+7}{2x-2}\).
 Rozwiązanie zadania
Rozwiązanie zadania
Mamy do czynienia z funkcją homograficzną. Jej wykresem jest hiperbola. W takich przypadkach najczęściej dzielimy wielomiany występujące w liczniku i mianowniku. Wykonajmy więc takie dzielenie:
\((-4x+7):(2x-2)=-2\)
\(\underline{-4x+4}\)
\(\ R=3\)
Otrzymaliśmy resztę z dzielenia. Wynik zapisujemy w następujący sposób:
\(y=\frac{-4x+7}{2x-2}=-2+\frac{3}{2x-2}\)
Sprowadzimy naszą funkcję do postaci \(f(x)=\frac{a}{x}\):
\(y=-2+\frac{3}{2x-2}\)
\(y=-2+\frac{3}{2(x-1)}\)
\(y+2=\frac{\frac{3}{2}}{x-1}\)
Aby naszkicować wykres tej funkcji skorzystamy z wiedzy na temat przesuwania wykresu funkcji w układzie współrzędnych o zadany wektor.
Wykres funkcji \(y=f(x)\) przesunięty w układzie współrzędnych o wektor \([p,q]\) ma wzór:
Jeżeli \(y=\frac{\frac{3}{2}}{x}\), to \(f(x-p)=\frac{\frac{3}{2}}{x-p}\). Zapiszemy naszą funkcję w następującej postaci
\(y-q=f(x-p)\)
\(y-(-2)=\frac{\frac{3}{2}}{x-1}\)
\(p=1, q=-2\)
Wystarczy więc przesunąć wykres funkcji \(y=\frac{\frac{3}{2}}{x}\) w układzie współrzędnych o wektor \(\vec{v}=[1,-2]\). Poniżej tabelka zmienności funkcji dla funkcji \(y=\frac{\frac{3}{2}}{x}\):
| \(x\) | 1 | -1 | 1/2 | -1/2 | 3 | -3 |
| \(f(x)\) | 3/2 | -3/2 | 3 | -3 | 1/2 | -1/2 |
Sporządzamy wykres funkcji \(y=\frac{-4x+7}{2x-2}\):
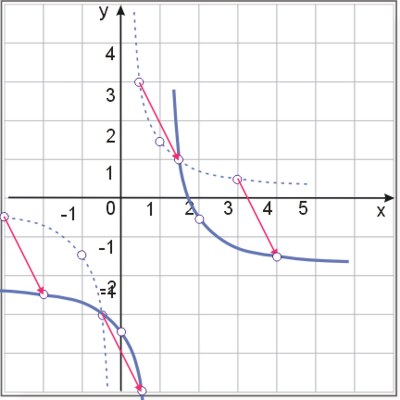
© medianauka.pl, 2009-12-30, ZAD-467


Zadania podobne

Zadanie nr 4 — maturalne.
Na rysunku przedstawiono fragment wykresu funkcji homograficznej f(x), której dziedziną jest zbiór \(D=(-\infty,3)\cup (3,+\infty)\).
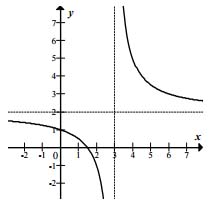
Równanie \(|f(x)|=p\) z niewiadomą \(x\) ma dokładnie jedno rozwiązanie
A. w dwóch przypadkach: \(p=0\) lub \(p=3\).
B. w dwóch przypadkach: \(p=0\) lub \(p=2\).
C. tylko wtedy, gdy \(p=3\).
D. tylko wtedy, gdy \(p=2\).

