Nauka » Matematyka » Wykres funkcji homograficznej

Zadanie maturalne nr 3, matura 2016 (poziom rozszerzony)

Na rysunku przedstawiono fragment wykresu funkcji homograficznej f(x), której dziedziną jest zbiór $D=(-\infty,3)\cup (3,+\infty)$ .
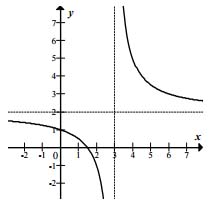
ilustracja do zadania maturalnego 3

Równanie |f(x)|=p z niewiadomą x ma dokładnie jedno rozwiązanie
A. w dwóch przypadkach: p=0 lub p=3
B. w dwóch przypadkach: p=0 lub p=2
C. tylko wtedy, gdy p=3
D. tylko wtedy, gdy p=2

Rozwiązanie zadania

Narysujmy najpierw wykres funkcji |f(x)|=p. Wartość funkcji znajduje się pod wartością bezwzględna, więc wszystkie ujemne wartości (części wykresu) odbijamy względem osi OX, aby uzyskać wartości dodatnie. Wykres naszej funkcji y=|f(x)| będzie wyglądał następująco:

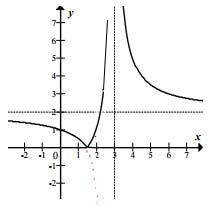
ilustracja - etap I

Mamy wykres funkcji y=|f(x)|, natomiast jak znaleźć rozwiązanie równania |f(x)|=p? Wystarczy znaleźć punkty wspólne wykresu naszej funkcji z prostą o równaniu y=p. Zmieniając wartość p, przesuwamy poziomą linię wykresu funkcji y=p w górę lub w dół. Badamy wówczas kiedy wykresy przecinają się w jednym punkcie. Ma to miejsce w dwóch przypadkach (patrze rysunek).

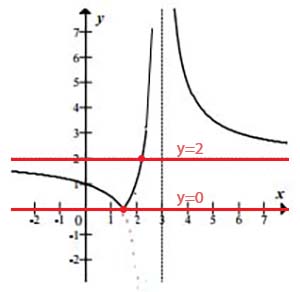
We wszystkich pozostałych przypadkach mamy do czynienia z dwoma punktami przecięcia się wykresów, a więc z dwoma rozwiązaniami równania. Mamy więc rozwiązanie zadania dla p=0 i p=2.

Odpowiedź

Odpowiedź B

Zadania podobne

Zadanie - wykres funkcji z wartością bezwzględną y=1/|x|
Sporządzić wykres funkcji $f(x)=\frac{1}{|x|}$

Pokaż rozwiązanie zadania

Zadanie - wykres funkcji z wartością bezwzględną y=1/|x+2|-3
Sporządzić wykres funkcji $f(x)=\frac{1}{|x+2|}-3$ .

Pokaż rozwiązanie zadania

Zadanie - wykres funkcji homograficznej y=(x-3)/(x-4)
Sporządzić wykres funkcji $y=\frac{x-3}{x-4}$

Pokaż rozwiązanie zadania

Zadanie - Wykres funkcji homograficznej y=(-4x+7)/(2x-2)
Sporządzić wykres funkcji:
$y=\frac{-4x+7}{2x-2}$

Pokaż rozwiązanie zadania

Niektóre treści nie są dostosowane do Twojego profilu. Jeżeli jesteś pełnoletni możesz wyrazić zgodę na przetwarzanie swoich danych osobowych. W ten sposób będziesz miał także wpływ na rozwój naszego serwisu.