Translacja o wektor
Co to jest translacja o wektor? Oto definicja translacji.
Translacja (przesunięcie równoległe) o wektor translacji \(\vec{w}\) jest to przekształcenie geometryczne płaszczyzny, w którym każdemu punktowi \(P\) przyporządkowujemy taki punkt \(P'\), że \(\vec{PP'}=\vec{w}\).
Poniższa animacja ilustruje translację.
Twierdzenie 1
Translacja jest przekształceniem izometrycznym, w którym obrazem dowolnego wektora jest wektor równy wektorowi translacji.
Twierdzenie 2
Przekształceniem odwrotnym do translacji o wektor \(\vec{w}\) jest translacja o wektor \(-\vec{w}\).
Twierdzenie 3
Złożeniem translacji o wektor \(\vec{w_1}\) oraz translacji o wektor \(\vec{w_2}\) jest translacja o wektor \(\vec{w_1}+\vec{w_2}\).
Twierdzenie 4
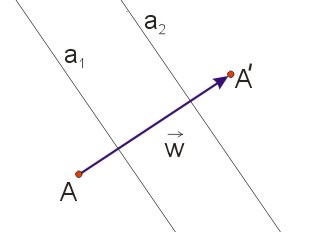
Translację o wektor \(\vec{w}\) można przedstawić jako złożenie dwóch symetrii osiowych, których osie są:
- równoległe między sobą i prostopadłe do wektora translacji,
- odległe od siebie o połowę długości wektora translacji,
- według zwrotu wektora translacji pierwsza oś poprzedza drugą.
Translacja — wzory
Poniżej przedstawiamy ujęcie analityczne translacji.
Obrazem punktu \(P=(x,y)\) w translacji o wektor \(\vec{w}=[a,b]\) jest punkt \(P'=(x',y')\). Między współrzędnymi zachodzi zależność:
\(x=x'-a\)
\(y=y'-b\)
Punkt \(P'\) ma zatem współrzędne: \(P'=(x+a,y+b)\).
Przykład
Znajdziemy równanie krzywej \(y=x^2+1\) w translacji o wektor \(\vec{w}=[1,-1]\).
Między współrzędnymi zachodzi zgodnie z tym, co napisano wyżej zależność:
\(x=x'-1\)
\(y=y'-(-1)=y'+1\)
Podstawiamy wyznaczone wartości zmiennych do równania krzywej i otrzymujemy obraz krzywej w tak zdefiniowanej translacji:
\(y=x^2+1\)
\(y'+1=(x'-1)^2+1\)
\(y'=x'^2-2x'+1+1-1\)
\(y'=x'^2-2x'+1\)
Zadania z rozwiązaniami
Zadanie nr 1.
Znaleźć obraz kwadratu \(ABCD\), gdzie \(A=(1,1), B=(2,3), C=(4,2), D=(3,0)\) w translacji o wektor \(\vec{w}=[-2,-1]\).
Zadanie nr 2.
Znaleźć obraz krzywej \(y=-x^2+x-1\) w translacji o wektor \(\vec{w}=[-2,1]\).
Zadanie nr 3.
Obrazem punktu \(P=(7,-3)\) w translacji o wektor \(\vec{w}\) jest punkt \(P'=(-3,7)\). Znaleźć współrzędne wektora translacji.
Inne zagadnienia z tej lekcji
Symetria osiowa
Przekształcenie geometryczne
Symetria środkowa
Symetria z poślizgiem
Rzut równoległy na prostą
Rzut prostokątny
Rzut równoległy na płaszczyznę
Symetralna odcinka
Obrót
Jednokładność
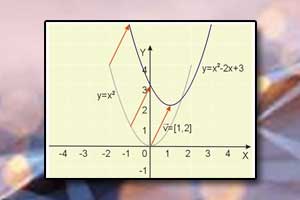Przesunięcie wykresu funkcji© medianauka.pl, 2010-11-28, A-1032
Data aktualizacji artykułu: 2023-07-16