Symetria osiowa
Co to jest symetria osiowa? Oto definicja.
Symetria osiowa względem prostej \(a\) jest to nietożsamościowa izometria płaszczyzny, w której każdy punkt prostej \(a\) jest punktem stałym.
Symetrię osiową względem prostej \(a\) oznaczamy następująco: \(S_a\). Prostą \(a\) nazywamy osią symetrii.
Przykłady
Zapis \(S_a(P)=P'\) czytamy następująco: „obrazem punktu P w symetrii osiowej względem prostej a jest punkt \(P'\).” lub „\(P'\) jest symetryczny do P względem prostej \(a\)”.
Zapis \(S_b(f)=f'\) czytamy następująco: „obrazem figury \(f\) w symetrii osiowej względem prostej \(b\) jest figura \(f'\).” lub „figura \(f'\) jest symetryczna do figury \(f\) względem prostej \(b\)”.
Przy danej prostej \(a\) oraz punkcie \(X\), który nie należy do tej prostej, znajdziemy jego obraz w symetrii osiowej względem \(a\).

Animacja

W powyższej animacji zaznaczono przerywaną linią prostą, która przechodzi przez punkt \(X\) i jego obraz \(X'\). Prosta ta (nazwijmy ją \(b\)) przecina oś symetrii (nazwijmy ten punkt \(P\)). Odległość punktu \(X\) od punktu przecięcia \(P\) zgodnie z definicją symetrii osiowej jest taka sama jak odległość obrazu \(X'\) od punktu \(P\).
Ponieważ \(S_a(X)=X', S_a(X')=X, S_a(P)=P\) to \(S_a(b)=b\). Stąd wynika, że \(|\angle APX|=|\angle APX'|\), więc \(a⊥b\).
Dwa punkty symetryczne względem prostej \(a\) leżą na prostej prostopadłej do \(a\), po przeciwnych stronach prostej \(a\) i w równych od niej odległościach.
Złożenie dwóch symetrii osiowych względem tej samej prostej jest przekształceniem tożsamościowym. Przekształceniem odwrotnym do \(S_a\) jest ta sama symetria osiowa.
W opisany wyżej sposób postępujemy, gdy szukamy obrazu figury geometrycznej w symetrii osiowej. Na poniższym filmie przedstawiono konstrukcję odcinka w symetrii osiowej.
Symetria osiowa — wzory
Przedstawiamy analityczne ujęcie symetrii osiowej.
Symetria osiowa względem osi OY
W symetrii osiowej względem osi \(OY\) obrazem pewnego punktu \(P=(x,y)\) jest punkt \(P'=(x',y')\). Zachodzą zależności między współrzędnymi punktu i jego obrazem:
\(x'=-x\)
\(y'=y\)
Symetria osiowa względem osi OX
W symetrii osiowej względem osi \(OX\) obrazem pewnego punktu \(P=(x,y)\) jest punkt \(P'=(x',y')\). Zachodzą zależności między współrzędnymi punktu i jego obrazem:
\(x'=x\)
\(y'=-y\)
Przykłady
Znajdziemy równanie krzywej \(y=x^2+1\) w symetrii względem osi OX oraz OY.
Korzystając z powyższych zależności między współrzędnymi punktu i jego obrazu w symetrii względem osi OX otrzymujemy:
\(y=x^2+1\)
\(-y'=x'^2+1/\cdot(-1)\)
\(y'=-x'^2-1\)
Korzystając z powyższych zależności między współrzędnymi punktu i jego obrazu w symetrii względem osi OY otrzymujemy:
\(y=x^2+1\)
\(y'=(-x')^2+1\)
\(y'=x'^2+1\)
W tym przypadku otrzymaliśmy tę samą krzywa. Oś OX jest więc osią symetrii tej krzywej.
Oś symetrii figury
Oś symetrii figury \(F\) nazywamy taką prostą \(p\), dla której obrazem figury \(F\) w symetrii osiowej względem prostej \(p\) jest ta sama figura:
\(S_p(F)=F\)
Figurę, która jest symetryczna sama do siebie względem pewnej osi symetrii, nazywamy figurą osiowo symetryczną.
Przykłady
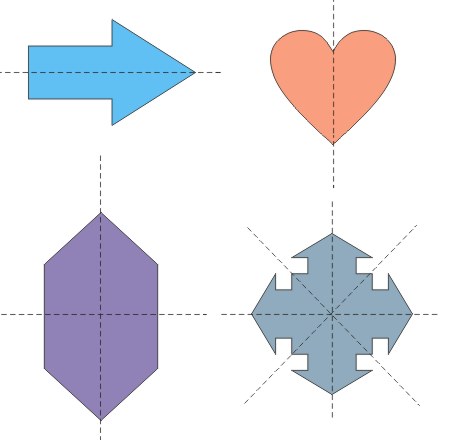
Na rysunku przedstawiono figury, które mają:
- pierwsza — jedną oś symetrii,
- druga — jedną oś symetrii,
- trzecia — dwie osie symetrii,
- czwarta — cztery osie symetrii.
Osie symetrii zostały zaznaczone przerywaną linią.
A oto inne przykłady:
- Prosta ma nieskończenie wiele osi symetrii — są to proste prostopadłe do danej prostej i dodatkowo ta sama prosta.
- Odcinek ma dwie osie symetrii — jedna jest jego symetralną, druga — prosta zawierająca dany odcinek.
- Okrąg i koło mają nieskończenie wiele osi symetrii — wszystkie przechodzą przez środek okręgu (koła).
Zadania z rozwiązaniami

Zadanie nr 1.
Znaleźć obraz kwadratu w symetrii osiowej względem prostej przechodzącej przez środki dwóch sąsiadujących boków tego kwadratu.

Zadanie nr 2.
Znaleźć obraz trójkąta prostokątnego w symetrii osiowej względem prostej przechodzącej przez tylko jeden z wierzchołków trójkąta równoległej do przyprostokątnej tego trójkąta.

Zadanie nr 3.
Znaleźć obraz trójkąta \(ABC\), gdzie \(A=(-2,3), B=(2,4), C=(2,-2)\) w symetrii osiowej względem osi \(OX\) i \(OY\).

Zadanie nr 4.
Znaleźć obraz krzywej \(y=3x^2-2x+1\) w symetrii osiowej względem osi \(OX\) i \(OY\).

Zadanie nr 5.
Znaleźć obraz okręgu \((x+2)^2+(y-1)^2=4\) w symetrii osiowej względem osi \(OY\). Sporządź odpowiednie wykresy w układzie współrzędnych.

Zadanie nr 6.
Znaleźć oś symetrii trójkąta \(ABC\), gdzie \(A=(1,1), B=(5,1), C=(3,3)\).

Zadanie nr 7 — maturalne.
Trójkąt \(ABC\) jest ostrokątny oraz \(|AC|>|BC|\). Dwusieczna \(d_C\) kąta \(ACB\) przecina bok \(AB\) w punkcie \(K\). Punkt \(L\) jest obrazem punktu \(K\) w symetrii osiowej względem dwusiecznej \(d_A\) kąta \(BAC\), punkt \(M\) jest obrazem punktu \(L\) w symetrii osiowej względem dwusiecznej \(d_C\) kąta \(ACB\), a punkt \(N\) jest obrazem punktu \(M\) w symetrii osiowej względem dwusiecznej \(d_B\) kąta \(ABC\) (zobacz rysunek).
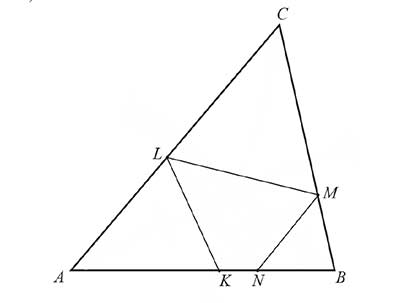
Udowodnij, że na czworokącie \(KNML\) można opisać okrąg.
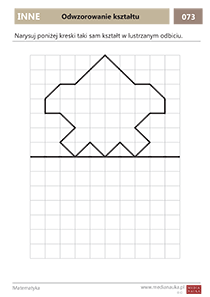
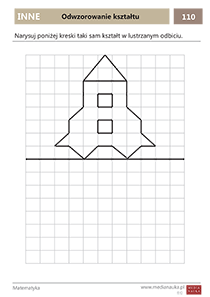
Wybrane karty pracy
Powiązane materiały
© medianauka.pl, 2010-11-03, A-1003
Data aktualizacji artykułu: 2023-07-15



 Przekształcenie geometryczne
Przekształcenie geometryczne Symetria środkowa
Symetria środkowa Symetria z poślizgiem
Symetria z poślizgiem Symetralna odcinka
Symetralna odcinka