Zadanie maturalne nr 5, matura 2018 (poziom rozszerzony)
Treść zadania:
Trójkąt \(ABC\) jest ostrokątny oraz \(|AC|>|BC|\). Dwusieczna \(d_C\) kąta \(ACB\) przecina bok \(AB\) w punkcie \(K\). Punkt \(L\) jest obrazem punktu \(K\) w symetrii osiowej względem dwusiecznej \(d_A\) kąta \(BAC\), punkt \(M\) jest obrazem punktu \(L\) w symetrii osiowej względem dwusiecznej \(d_C\) kąta \(ACB\), a punkt \(N\) jest obrazem punktu \(M\) w symetrii osiowej względem dwusiecznej \(d_B\) kąta \(ABC\) (zobacz rysunek).
Udowodnij, że na czworokącie \(KNML\) można opisać okrąg.
Rozwiązanie zadania
Kiedy można opisać okrąg na czworokącie? Okrąg można opisać na takim wielokącie, którego symetralne boków przecinają się w jednym punkcie, który stanowi właśnie środek tego okręgu.
Zamiast rozpatrywać czworokąt KLMN rozpatrzmy dwa trójkąty wyznaczone przez punkty KLMN po to, aby skorzystać z własności symetrii osiowej (mamy trzy dwusieczne).
Rozważmy trójkąt KLM. Z definicji symetrii osiowej wynika, że dwusieczna dA jest symetralną boku KL, a dwusieczna dC jest symetralną odcinka LM. Symetralne boków trójkąta przecinają się w jednym punkcie O, który jest środkiem okręgu opisanego na tym trójkącie. Czyli punkt wspólny dwusiecznych dA i dC (symetralnych boków trójkąta KLM) jest środkiem okręgu, którego promieniem jest odcinek OL.
Rozważmy teraz trójkąt LMN. Z definicji symetrii osiowej wynika, że dwusieczna dC jest symetralną boku LM. Analogicznie dwusieczna dB jest symetralną boku MN. Punkt wspólny tych dwusiecznych (symetralnych) jest tym samym punktem, o którym była mowa wyżej i jest środkiem okręgu opisanego na trójkącie LMN. Zatem musi to być ten sam okrąg.
Wszystkie wierzchołki czworokąta KNML leżą na tym okręgu. To kończy dowód.
© medianauka.pl, 2023-01-12, ZAD-4638


Zadania podobne
Zadanie nr 1.
Przez punkty \(A, B\) na okręgu o promieniu \(r=2,5\) poprowadzono średnicę. Punkt \(D\) leży na okręgu tak, że \(|BD|=4\). Oblicz odległość \(|AD|\).
Zadanie nr 2.
Na średnicy okręgu o promieniu długości 6 obrano punkt \(A\) w taki sposób, że punkt ten dzieli promień okręgu w stosunku 1 do 2 (krótszy odcinek znajduje się bliżej okręgu). Obliczyć obwód trójkątów wyznaczonych przez średnicę i odcinek prostopadłej przechodzący przez punkt \(A\).

Zadanie nr 4 — maturalne.
Punkty \(ABCD\) leżą na okręgu o środku \(S\) (zobacz rysunek). Miara kąta \(BDC\) jest równa:
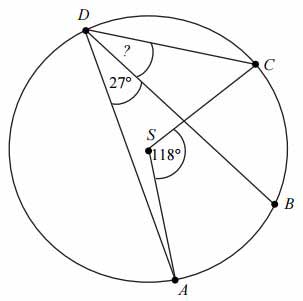
A. 91°
B. 72,5°
C. 18°
D. 32°

Zadanie nr 5 — maturalne.
Miara kąta wpisanego w okrąg jest o \(20°\) mniejsza od miary kąta środkowego opartego na tym samym łuku. Wynika stąd, że miara kąta wpisanego jest równa:
A. \(5°\)
B. \(10°\)
C. \(20°\)
D. \(30°\)

Zadanie nr 6 — maturalne.
Środek \(S\) okręgu opisanego na trójkącie równoramiennym \(ABC\), o ramionach \(AC\) i \(BC\), leży wewnątrz tego trójkąta (zobacz rysunek).
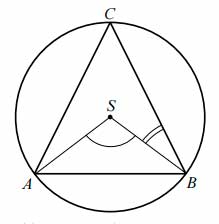
Wykaż, że miara kąta wypukłego \(ASB\) jest cztery razy większa od miary kąta wypukłego \(SBC\).

Zadanie nr 7 — maturalne.
Na okręgu o środku w punkcie \(O\) leży punkt \(C\) (zobacz rysunek). Odcinek \(AB\) jest średnicą tego okręgu. Zaznaczony na rysunku kąt środkowy \(\alpha\) ma miarę:
A. \(m=116°
B. \(m=114°
C. \(m=112°
D. \(m=110°

Zadanie nr 8 — maturalne.
Dany jest okrąg o środku \(S\). Punkty \(K, L\) i \(M\) leżą na tym okręgu. Na łuku \(KL\) tego okręgu są oparte kąty \(KSL\) i \(KML\) (zobacz rysunek), których miary \(\alpha\) i \(\beta\), spełniają warunek \(\alpha +\beta=111°\). Wynika stąd, że
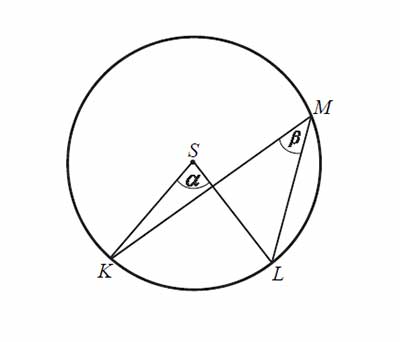
A. \(\alpha=74°\)
B. \(\alpha=76°\)
C. \(\alpha=70°\)
D. \(\alpha=72°\)

Zadanie nr 9 — maturalne.
Okręgi o środkach odpowiednio \(A\) i \(B\) są styczne zewnętrznie i każdy z nich jest styczny do obu ramion danego kąta prostego (zobacz rysunek). Promień okręgu o środku \(A\) jest równy 2.
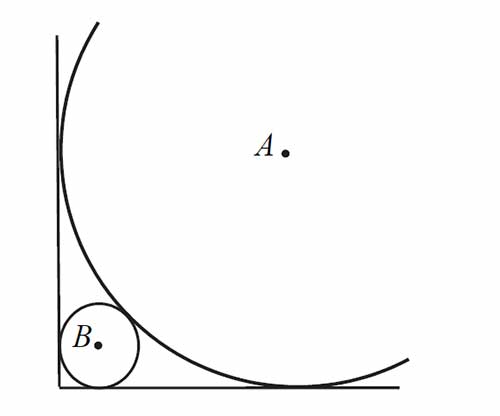
Uzasadnij, że promień okręgu o środku \(B\) jest mniejszy od \(\sqrt{2}-1\).

Zadanie nr 10 — maturalne.
Punkty \(D\) i \(E\) leżą na okręgu opisanym na trójkącie równobocznym \(ABC\) (zobacz rysunek). Odcinek \(CD\) jest średnicą tego okręgu. Kąt wpisany \(DEB\) ma miarę \(\alpha\).
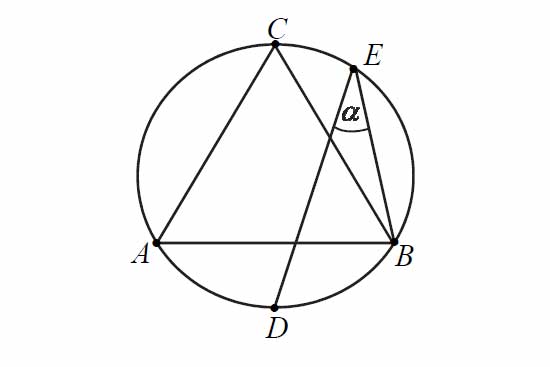
A. \(\alpha=30°\)
B. \(\alpha<30°\)
C. \(\alpha>45°\)
D. \(\alpha=45°\)

Zadanie nr 11 — maturalne.
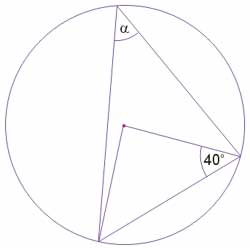
Punkty \(A, B, C, D\) leżą na okręgu o środku w punkcie \(O\). Kąt środkowy \(DOC\) ma miarę 118° (zobacz rysunek).

Miara kąta ABC jest równa
A. 59°
B. 48°
C. 62°
D. 31°

Zadanie nr 12 — maturalne.
Punkty A, B, C leżą na okręgu o środku S. Punkt D jest punktem przecięcia cięciwy AC i średnicy okręgu poprowadzonej z punktu B. Miara kąta BSC jest równa α, a miara kąta ADB jest równa γ (zobacz rysunek).
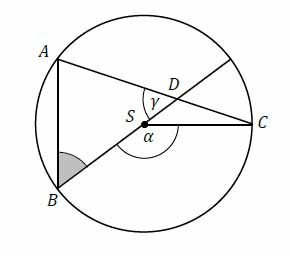
Wtedy kąt ABD ma miarę
A. \(\frac{\alpha}{2}+\gamma−180°\)
B. \(180°-\frac{\alpha}{2}-\gamma\)
C. \(180°-\alpha-\gamma\)
D. \(\alpha+\gamma−180°\)

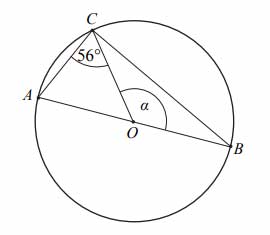
Zadanie nr 13 — maturalne.
Punkty \(A, B, C\) leżą na okręgu o środku w punkcie \(O\). Kąt \(ACO\) ma miarę 70° (zobacz rysunek). Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. Miara kąta ostrego \(ABC\) jest równa:
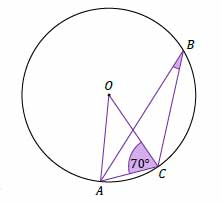
A. \(10°\)
B. \(20°\)
C. \(35°\)
D. \(40°\)