Symetria środkowa
Co to jest symetria środkowa? Oto definicja tego przekształcenia.
Symetria środkowa względem punktu \(O\), nazywanego środkiem symetrii, jest to przekształcenie płaszczyzny polegające na tym, że punkt \(O\) jest punktem niezmienniczym tego przekształcenia, a obrazem dowolnego innego punktu \(A\) jest punkt \(A'\) taki, że punkt \(O\) jest środkiem odcinka \(\overline{AA'}\).
Poniższa animacja ilustruje symetrię środkową na przykładzie szukania obrazu punktu \(A\) w tym przekształceniu.

Animacja

Symetrię osiową względem punktu \(O\) oznaczamy następująco: \(S_O\), natomiast zapis \(S_O(A)=A'\) czytamy w następujący sposób: „obrazem punktu \(A\) w symetrii środkowej jest punkt \(A'\)”.
Poniższa ilustracja pokazuje symetrię środkową pewnej figury ABCDE.
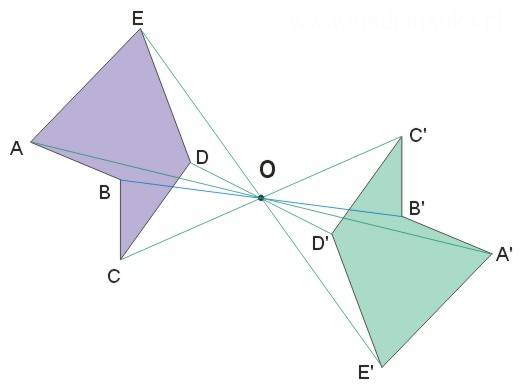
Twierdzenie 1
Symetria środkowa względem punktu \(O\) jest złożeniem dwóch symetrii osiowych względem prostych prostopadłych przecinających się w punkcie \(O\).
Ilustruje to poniższy rysunek:
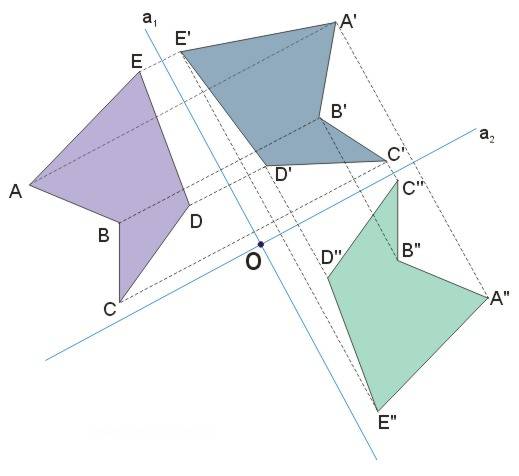
Twierdzenie 2
Symetria środkowa względem punktu \(O\) jest obrotem o kąt półpełny dookoła punktu \(O\).
Ilustruje to poniższy rysunek:
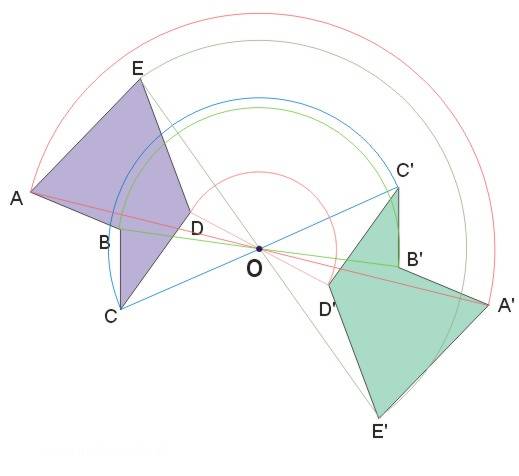
Środek symetrii figury
co to jest środek symetrii figury? Oto definicja,
Jeżeli istnieje taki punkt \(O\), że obrazem figury \(f\) w symetrii środkowej względem tego punktu jest ta sama figura, to punkt ten nazywamy środkiem symetrii figury \(f\), a figurę nazywamy środkowosymetryczną.
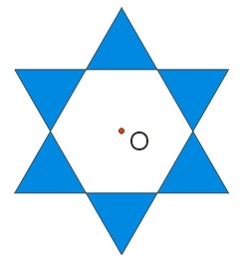
Przykłady
Do figur środkowosymetrycznych należą:
- Okrąg — środkiem symetrii jest środek okręgu.
- Koło — środkiem symetrii jest środek koła.
- Prosta — środkiem symetrii jest dowolny punkt prostej.
- Kwadrat — środkiem symetrii jest punkt przecięcia się przekątnych kwadratu.
A oto inne przykłady figur środkowosymetrycznych:
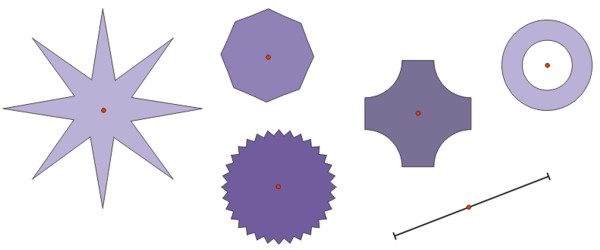
Symetria środkowa względem początku układu współrzędnych — wzory
A oto ujęcie analityczne symetrii środkowej.
W symetrii środkowej względem początku układu współrzędnych obrazem pewnego punktu \(P=(x,y)\) jest punkt \(P'=(x',y')\). Zachodzą zależności między współrzędnymi punktu i jego obrazem:
\(x'=-x\)
\(y'=-y\)
Przykład
Znajdziemy równanie krzywej \(y=x^2+1\) w symetrii względem początku układu współrzędnych.
Korzystając z powyższych zależności między współrzędnymi punktu i jego obrazu w symetrii środkowej otrzymujemy:
\(y=x^2+1\)
\(-y'=(-x')^2+1/\cdot(-1)\)
\(y'=-x'^2-1\)
Pytania
Gdzie leży środek symetrii kwadratu?
Środkiem symetrii w kwadracie leży na punkcie przecięcia się jego przekątnych.
Zadania z rozwiązaniami

Zadanie nr 1.
Znaleźć obraz trójkąta równobocznego w symetrii środkowej względem dowolnego wierzchołka tego trójkąta.

Zadanie nr 2.
Znaleźć obraz kwadratu w przekształceniu będącym złożeniem czterech symetrii środkowych względem kolejnych wierzchołków tego kwadratu.

Zadanie nr 3.
Znaleźć obraz trójkąta \(BC\) w symetrii środkowej względem początku układu współrzędnych, jeżeli \(A=(-2,3), B=(5,3), C=(0,7)\).

Zadanie nr 4.
Znaleźć obraz krzywej \(y=x^3-x^2\) w symetrii środkowej względem początku układu współrzędnych.

Zadanie nr 5 — maturalne.
Dane są punkty \(M = (-2,1), N = (-1,3)\). Punkt \(K \)jest środkiem odcinka \(MN\). Obrazem punktu \(K\) w symetrii względem początku układu współrzędnych jest punkt:
A. \(K'=(2,-\frac{3}{2})\)
B. \(K'=(2,\frac{3}{2})\)
C. \(K'=(\frac{3}{2},2)\)
D. \(K'=(\frac{3}{2},-2)\)

Zadanie nr 6 — maturalne.
Na rysunku przedstawiony jest fragment wykresu funkcji liniowej f. Na wykresie tej funkcji leżą punkty \(A=(0,4)\) i \(B=(2,2)\).
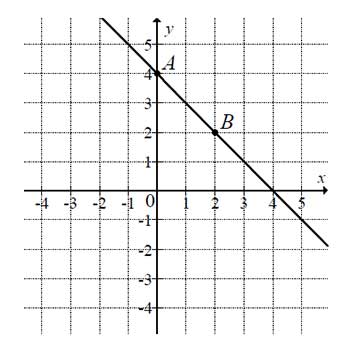
Obrazem prostej \(AB\) w symetrii względem początku układu współrzędnych jest wykres funkcji \(g\) określonej wzorem
A. \(g(x)=x+4\)
B. \(g(x)=x-4\)
C. \(g(x)=-x-4\)
D. \(g(x)=-x+4\)

Zadanie nr 7 — maturalne.
Punkt B jest obrazem punktu \(A=(−3,5)\) w symetrii względem początku układu współrzędnych. Długość odcinka \(AB\) jest równa
A. \(2\sqrt{34}\)
B. \(8\)
C. \(\sqrt{34}\)
D. \(12\)
Powiązane materiały
Ćwiczenia, sprawdziany i quizy
 Symetria środkowa
Symetria środkowa© medianauka.pl, 2010-11-21, A-1021
Data aktualizacji artykułu: 2023-07-16

 Symetria osiowa
Symetria osiowa Przekształcenie geometryczne
Przekształcenie geometryczne Symetria z poślizgiem
Symetria z poślizgiem Symetralna odcinka
Symetralna odcinka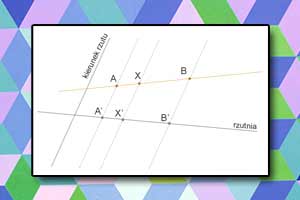 Rzut równoległy na prostą
Rzut równoległy na prostą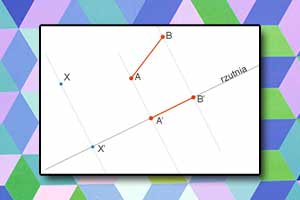 Rzut prostokątny
Rzut prostokątny Rzut równoległy na płaszczyznę
Rzut równoległy na płaszczyznę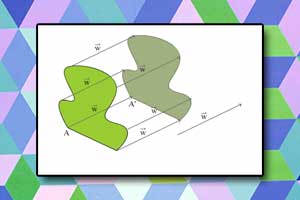 Translacja
Translacja Obrót
Obrót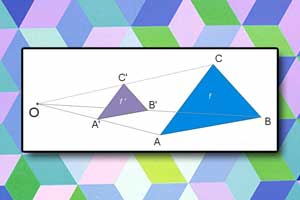 Jednokładność
Jednokładność



