
Zadanie maturalne nr 19, matura 2019
Treść zadania:
Na rysunku przedstawiony jest fragment wykresu funkcji liniowej f. Na wykresie tej funkcji leżą punkty \(A=(0,4)\) i \(B=(2,2)\).
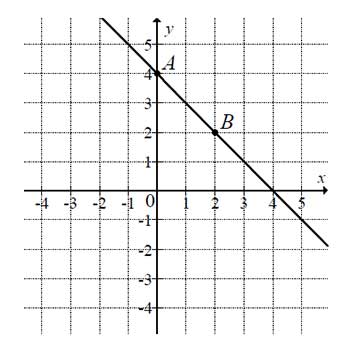
Obrazem prostej \(AB\) w symetrii względem początku układu współrzędnych jest wykres funkcji \(g\) określonej wzorem
A. \(g(x)=x+4\)
B. \(g(x)=x-4\)
C. \(g(x)=-x-4\)
D. \(g(x)=-x+4\)
 Rozwiązanie zadania
Rozwiązanie zadania
W symetrii środkowej względem początku układu współrzędnych obrazem pewnego punktu P=(x,y) jest punkt P'=(x',y'). Zachodzą zależności między współrzędnymi punktu i jego obrazem:
Zatem obrazem danych punktów w symetrii względem początku układu współrzędnych jest:
A=(0,4) i B=(2,2)
A'=(0,-4) i B'=(-2,-2)
Znajdziemy teraz równanie prostej g(x)=ax+b:
\(\begin{cases} -4=a\cdot 0 +b\\ -2=a\cdot -2 + b\end{cases}\)
\(\begin{cases} b=-4\\ -2=-2a-4\end{cases}\)
\(\begin{cases} b=-4\\ 2a=-2\end{cases}\)
\(\begin{cases} b=-4\\ a=-1\end{cases}\)
Zatem:
\(g(x)=-x-4\)
 Odpowiedź
Odpowiedź
© medianauka.pl, 2023-01-30, ZAD-4665


Zadania podobne
Zadanie nr 1.
Znaleźć obraz trójkąta równobocznego w symetrii środkowej względem dowolnego wierzchołka tego trójkąta.
Zadanie nr 2.
Znaleźć obraz kwadratu w przekształceniu będącym złożeniem czterech symetrii środkowych względem kolejnych wierzchołków tego kwadratu.
Zadanie nr 3.
Znaleźć obraz trójkąta \(BC\) w symetrii środkowej względem początku układu współrzędnych, jeżeli \(A=(-2,3), B=(5,3), C=(0,7)\).
Zadanie nr 4.
Znaleźć obraz krzywej \(y=x^3-x^2\) w symetrii środkowej względem początku układu współrzędnych.

Zadanie nr 5 — maturalne.
Dane są punkty \(M = (-2,1), N = (-1,3)\). Punkt \(K \)jest środkiem odcinka \(MN\). Obrazem punktu \(K\) w symetrii względem początku układu współrzędnych jest punkt:
A. \(K'=(2,-\frac{3}{2})\)
B. \(K'=(2,\frac{3}{2})\)
C. \(K'=(\frac{3}{2},2)\)
D. \(K'=(\frac{3}{2},-2)\)

Zadanie nr 6 — maturalne.
Punkt B jest obrazem punktu \(A=(−3,5)\) w symetrii względem początku układu współrzędnych. Długość odcinka \(AB\) jest równa
A. \(2\sqrt{34}\)
B. \(8\)
C. \(\sqrt{34}\)
D. \(12\)

