Jednokładność
Jednokładność o środku \(O\) i skali \(k\neq 0\) jest to przekształcenie płaszczyzny, które dowolnemu punktowi \(A\) przyporządkowuje taki punkt \(A'\), że \(\overline{OA'}=k\cdot \overline{OA}\).
Przykład
Poniższy rysunek przedstawia jednokładność figury \(f\) w skali \(k=\frac{1}{2}\).
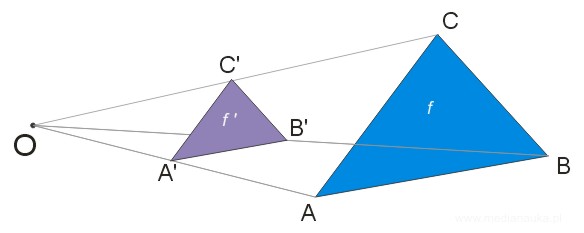
Właściwości jednokładności
Cechy jednokładności o środku \(O\):
- Jednokładność o skali \(k=1\) jest przekształceniem tożsamościowym (to znaczy, że obrazem figury w takim przekształceniu jest ta sama figura).
- Jednokładność o skali \(k=-1\) jest symetrią środkową.
- Przekształcenie odwrotne do jednokładności o skali \(k\) jest jednokładność o skali \(\frac{1}{k}\).
- Złożenie dwóch jednokładności o skalach \(k_1, k_2\) jest jednokładnością o skali \(k_1k_2\), to oznacza, że złożenie jednokładności nie zależy od kolejności przekształceń.
- Jednokładność nie jest przekształceniem izometrycznym (jest izometrią tylko w przypadku, gdy \(k=1\) lub \(k=-1\)).
- Obrazem wektora \(\vec{w}\) w jednokładności o skali \(k\) jest wektor równy wektorowi \(k\vec{w}\).
- Jednokładność zachowuje współliniowość i uporządkowanie punktów.
- Jednokładność zachowuje równoległość prostych.
- Jednokładność przekształca kąt w kąt przystający do danego kąta i kąt skierowany w równy mu kąt skierowany.
- Jednokładność zachowuje stosunek odcinków.
- Obrazem środka odcinka w jednokładności jest środek odcinka.
- Obrazem okręgu w jednokładności jest okrąg.
Jednokładność — wzory
A oto ujęcie analityczne jednokładności.
W jednokładności o środku \(O\) (początek układu współrzędnych) i różnej od zera skali \(k\) obrazem pewnego punktu \(P=(x,y)\) jest punkt \(P'=(x',y')\). Zachodzą zależności między współrzędnymi punktu i jego obrazem:
\(x'=kx\)
\(y'=ky\)
oraz
\(x=\frac{1}{k}x'\)
\(y=\frac{1}{k}y'\)
Przykład
Znajdziemy równanie krzywej \(y=x^2+1\) w jednokładności o skali \(k=\frac{1}{3}\).
Korzystając z powyższych zależności między współrzędnymi punktu i jego obrazu otrzymujemy:
\(y=x^2+1\)
\(\frac{1}{\frac{1}{3}}y'=[\frac{1}{\frac{1}{3}}x']^2+1\)
\(3y'=(3x')^2+1\)
\(3y'=9x'^2+1/:3\)
\(y'=3x'^2+\frac{1}{3}\)
Zadania z rozwiązaniami

Zadanie nr 1.
Znaleźć obraz kwadratu w jednokładności o środku w jednym z wierzchołków tego kwadratu i skali \(k=2\).

Zadanie nr 2.
Znaleźć obraz trójkąta prostokątnego w jednokładności o środku w punkcie, który jest środkiem przeciwprostokątnej tego trójkąta i skali \(k=-\frac{1}{2}\).

Zadanie nr 3.
Znaleźć obraz odcinka \(\overline{AB}\), gdzie \(A=(-1,2), B=(-2,-3)\) w jednokładności o środku w początku układu współrzędnych i skali \(k=3\). Zilustrować to przekształcenie w układzie współrzędnych.

Zadanie nr 4.
Znaleźć obraz krzywej \(y=x^2\) w jednokładności o środku w początku układu współrzędnych i skali \(k=\frac{1}{2}\). Zilustrować to przekształcenie w układzie współrzędnych.

Zadanie nr 5 — maturalne.
Prosta o równaniu \(x+y−10=0\) przecina okrąg o równaniu \(x^2+y^2−8x−6y+8=0\) w punktach \(K\) i \(L\). Punkt \(S\) jest środkiem cięciwy \(KL\). Wyznacz równanie obrazu tego okręgu w jednokładności o środku \(S\) i skali \(k=−3\).
Powiązane materiały
© medianauka.pl, 2010-12-04, A-1039
Data aktualizacji artykułu: 2023-07-17

 Symetria osiowa
Symetria osiowa Przekształcenie geometryczne
Przekształcenie geometryczne Symetria środkowa
Symetria środkowa Symetria z poślizgiem
Symetria z poślizgiem Rzut równoległy na prostą
Rzut równoległy na prostą Rzut prostokątny
Rzut prostokątny Rzut równoległy na płaszczyznę
Rzut równoległy na płaszczyznę Symetralna odcinka
Symetralna odcinka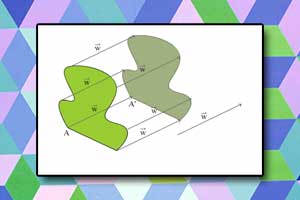 Translacja
Translacja Obrót
Obrót