Rzut równoległy na płaszczyznę
Dany jest układ rzutowania:
- płaszczyzna, którą będziemy nazywać płaszczyzną rzutów lub rzutnią,
- prosta (kierunek rzutu), która nie jest równoległa do rzutni.
Każda prosta równoległa do kierunku rzutu nazywamy prostą rzutującą.
Rzut równoległy na płaszczyznę jest to przekształcenie geometryczne przestrzeni w płaszczyznę, określone tak, że przez dowolny punkt \(P\) przestrzeni prowadzimy prostą rzutującą, która przecina rzutnię w punkcie \(P'\), który jest obrazem punktu \(P\) w tym przekształceniu lub rzutem punktu \(P\) na płaszczyznę.
Poniższa animacja ilustruje przekształcenie punktu \(P\) w kierunku \(k\) na płaszczyznę \(\sigma\).

Animacja

Punktem stałym (czyli takim, który jest obrazem samego siebie w danym przekształceniu) opisanego wyżej przekształcenia jest dowolny punkt płaszczyzny.
Aby zrzutować figurę na płaszczyznę w danym kierunku, należy zrzutować każdy punkt tej figury.
Twierdzenie
- Obrazem prostej nierównoległej do kierunku rzutu jest prosta.
- Obrazem prostej równoległej do kierunku rzutu jest punkt.
- Rzut odcinka na płaszczyznę jest odcinkiem lub punktem.
- Rzut środka odcinka na płaszczyznę jest środkiem obrazu tego odcinka.
- Rzuty wektorów równych na płaszczyznę są wektorami równymi.
- Jeżeli punkt \(C\) leży między punktami \(A, B\) i wszystkie te punkty leżą na prostej nierównoległej do kierunku rzutu \(k\), to obraz \(C'\) leży między obrazami \(A', B'\) w rzucie na płaszczyznę w kierunku \(k\).
Rzut równoległy ukośny
Rzut równoległy ukośny jest to rzut równoległy na płaszczyznę, w którym kierunek rzutu nie jest prostopadły do płaszczyzny rzutów.
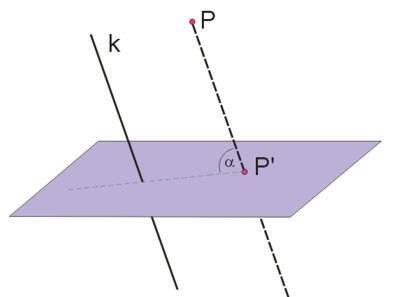
Ten rodzaj rzutu służy do przedstawiania brył na płaszczyźnie (na płaskim rysunku). Ilustruje to poniższy rysunek.
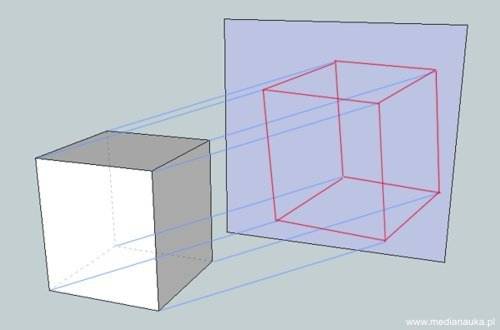
Rzut równoległy prostokątny
Rzut równoległy prostokątny jest to rzut równoległy na płaszczyznę, w którym kierunek rzutu jest prostopadły do płaszczyzny rzutów.
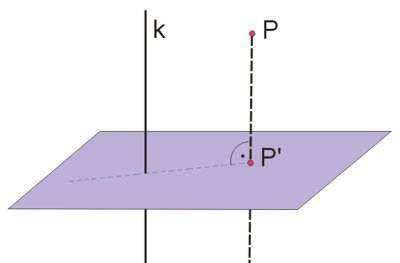
Definicja
Odległość punktu \(P\) od płaszczyzny jest to odległość punktu \(P\) od rzutu prostokątnego tego punktu na daną płaszczyznę.
Powiązane materiały
© medianauka.pl, 2011-08-02, A-1397
Data aktualizacji artykułu: 2023-07-15

 Przekształcenie geometryczne
Przekształcenie geometryczne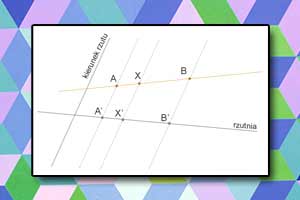 Rzut równoległy na prostą
Rzut równoległy na prostą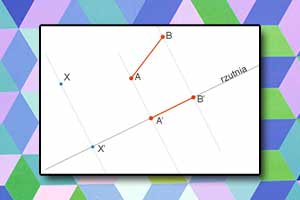 Rzut prostokątny
Rzut prostokątny