Odcinek
Definicja
Odcinek \(\overline{AB}\) jest to zbiór punktów, leżących na prostej między punktami \(A\) i \(B\) wraz z punktami \(A\) i \(B\).
Punkty \(A\) i \(B\) nazywamy końcami odcinka.
Jeżeli punkty \(A=B\) to odcinek \(\overline{AB}\) nazywamy zerowym.
Twierdzenie
\(X\in \overline{AB}\Leftrightarrow |AX|+|XB|=|AB|\)
Powyższe zdanie logiczne możemy przeczytać następująco: punkt \(X\) należy do odcinka \(\overline{AB}\) wtedy i tylko wtedy, gdy suma odległości między punktami \(A, X\) oraz \(X, B\) jest równa odległości między punktami \(A\) i \(B\).
Długość odcinka
Odległość \(|AB|\) będziemy nazywać długością odcinka. Zatem długość odcinka jest to odległość między jego końcami. Długość odcinka zerowego jest równa 0.
Odcinki nazywamy równymi, jeżeli mają taką samą długość.
Często zdarza się, że odcinki oznaczamy jedną literą. Stosujemy wówczas małe litery, np. \(\overline{a},\ \overline{b},\ \overline{c}\). W takim przypadku długość odcinka oznaczamy odpowiednio: \(|a|, |b|, |c|\) lub po prostu \(a, b, c\).
Aksjomat
Na każdej półprostej leży dokładnie jeden punkt, którego odległość od początku tej półprostej równa się danej liczbie nieujemnej.
Tłumacząc to sformułowanie, można powiedzieć, że na każdej półprostej można odłożyć odcinek równy danemu odcinkowi, albo inaczej: istnieją odcinki o dowolnej długości.
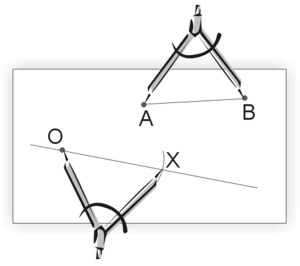
Co to znaczy odłożyć odcinek na prostej lub półprostej od punktu \(O\)? To znaczy wyznaczyć na tej prostej taki punkt \(X\), którego odległość od punktu \(O\) jest równa długości tego odcinka. Odkładanie odcinka zostało zilustrowane rysunkiem obok.
Poniżej przedstawiono przykład konstrukcji odcinka:
Zadanie
Skonstruuj odcinek o długości \(1,5\), jeśli \(|PQ|=1\).
Odpowiedź jest zilustrowana filmem:
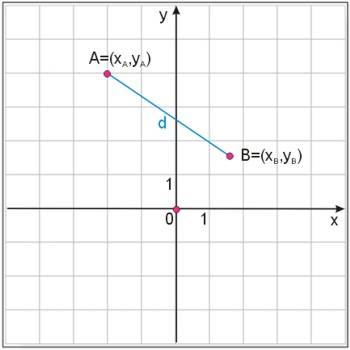
Wzór na długość odcinka
Długość odcinka w układzie współrzędnych jest równa odległości końców odcinka \(A=(x_A,y_A), \ B=(x_B, y_B)\) i obliczamy ją ze wzoru:
Wzór wynika bezpośrednio z twierdzenia Pitagorasa.
Przykład
Dane są punkty: \(A=(1,2), B=(-1,4)\). Obliczyć długość odcinka \(\overline{AB}\).
Korzystamy z powyższego wzoru:
\(|AB|=\sqrt{(-1-1)^2+(4-2)^2}=\sqrt{4+4}=\sqrt{8}=2\sqrt{2}\)
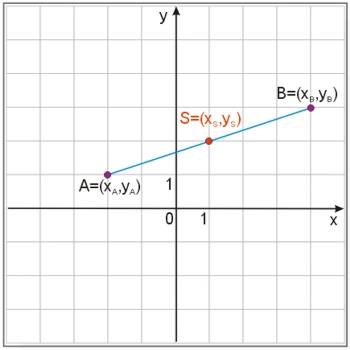
Wzór na środek odcinka
Jeżeli końce odcinka \(\overline{AB}\) mają współrzędne: \(A=(x_A,y_A), \ B=(x_B, y_B)\), to współrzędne środka odcinka i obliczamy ją ze wzoru:
Powyższy wzór na środek odcinka wykorzystamy w poniższym przykładzie zadania:
Przykład
Dane są punkty: \(A=(1,2), B=(-1,4)\). Obliczyć współrzędne środka odcinka \(\overline{AB}\).
Korzystamy z powyższego wzoru:
\(x_S=\frac{1-1}{2}=0,\quad{}y_S=\frac{2+4}{2}=3\)
\(S=(0,3)\)
Ćwiczenia
Ćwiczenia interakcyjne pomogą przygotować się na sprawdzian, test, egzamin, a ponadto usystematyzują wiedzę z danej dziedziny. To także świetny trening do matury. Wiele ćwiczeń to dobre zadania maturalne.
Zadania z rozwiązaniami
Zadanie nr 1.
Dane są punkty \(A=(-3,-2), B=(2, -2)\). Obliczyć długość odcinka \(\overline{AB}\).
Zadanie nr 2.
Dany jest punkt \(A=(1,4)\). Znaleźć taki punkt \(B\), że \(|\overline{AB}|=1\) i który leży na prostej \(x=\frac{1}{2}\).
Zadanie nr 3.
Obliczyć pole i obwód trójkąta prostokątnego, wyznaczonego przez punkty \(A=(1,2), B=(1,3), C=(4,1)\).
Zadanie nr 4.
Dany jest odcinek o końcach \(A=(2+\sqrt{2}, 2), \ B=(-4+\sqrt{2}, -4)\). Znaleźć współrzędne środka odcinka \(\overline{AB}\).
Zadanie nr 5.
Znaleźć środek kwadratu wyznaczonego przez punkty \(A=(0,0), B=(1,2), C=(3,1), D=(2,-1)\).
Zadanie nr 6 — maturalne.
W układzie współrzędnych dane są punkty \(A=(a,6)\) oraz \(B=(7,b)\). Środkiem odcinka \(AB\) jest punkt \(M=(3,4)\). Wynika stąd, że:
A. \(a=5\) i \(b=5\)
B. \(a=-1\) i \(b=2\)
C. \(a=4\) i \(b=10\)
D. \(a=-4\) i \(b=-2\)
Zadanie nr 7 — maturalne.
Punkty \(A=(30,32)\) i \(B=(0,8)\) są sąsiednimi wierzchołkami czworokąta \(ABCD \) wpisanego w okrąg. Prosta o równaniu \(x-y+2=0\) jest jedyną osią symetrii tego czworokąta i zawiera przekątną \(AC\). Oblicz współrzędne wierzchołków \(C\) i \(D\) tego czworokąta.
Zadanie nr 8 — maturalne.
Punkt \(A=(7,−1)\) jest wierzchołkiem trójkąta równoramiennego \(ABC\), w którym \(|AC|=|BC|\). Obie współrzędne wierzchołka \(C\) są liczbami ujemnymi. Okrąg wpisany w trójkąt ABC ma równanie \(x^2+y^2=10\). Oblicz współrzędne wierzchołków \(B\) i \(C\) tego trójkąta.
Zadanie nr 9 — maturalne.
Dane są punkty o współrzędnych \(A=(−2, 5)\) oraz \(B=(4, −1)\). Średnica okręgu wpisanego
w kwadrat o boku \(AB\) jest równa
A. \(12\)
B. \(6\)
C. \(6\sqrt{2}\)
D. \(2\sqrt{6}\)
Zadanie nr 10 — maturalne.
Dany jest punkt \(A=(−18,10)\). Prosta o równaniu \(y=3x\) jest symetralną odcinka \(AB\). Wyznacz współrzędne punktu \(B\).
Zadanie nr 11 — maturalne.
Punkt B jest obrazem punktu \(A=(−3,5)\) w symetrii względem początku układu współrzędnych. Długość odcinka \(AB\) jest równa
A. \(2\sqrt{34}\)
B. \(8\)
C. \(\sqrt{34}\)
D. \(12\)
Zadanie nr 12 — maturalne.
Punkty \(K=(4,−10)\) i \(L=(b,2)\) są końcami odcinka \(KL\). Pierwsza współrzędna środka odcinka \(KL\) jest równa (−12). Wynika stąd, że
A. \(b=-28\)
B. \(b=-14\)
C. \(b=-24\)
D. \(b=-10\)
Zadanie nr 13.
Znaleźć równanie symetralnej odcinka \(\overline{AB}\), gdzie \(A=(1,4), \ B=(-2, 1)\).
Zadanie nr 14 — maturalne.
Parabola o równaniu \(y=2-\frac{1}{2}x^2\) przecina oś \(Ox\) układu współrzędnych w punktach \(A=(- 2,0)\) i \(B=(2,0)\). Rozpatrujemy wszystkie trapezy równoramienne \(ABCD\), których dłuższą podstawą jest odcinek \(AB\), a końce \(C\) i \(D\) krótszej podstawy leżą na paraboli (zobacz rysunek).
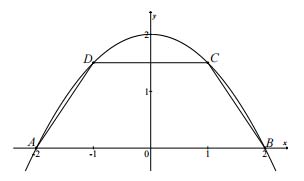
Wyznacz pole trapezu \(ABCD\) w zależności od pierwszej współrzędnej wierzchołka \(C\). Oblicz współrzędne wierzchołka \(C\) tego z rozpatrywanych trapezów, którego pole jest największe.
Zadanie nr 15 — maturalne.
Odległość początku układu współrzędnych od prostej o równaniu \(y = 2x + 4\) jest równa
A. \(\frac{\sqrt{5}}{5}\)
B. \(\frac{4\sqrt{5}}{5}\)
C. \(\frac{4}{5}\)
D. \(4\)
Inne zagadnienia z tej lekcji
Aksjomaty planimetrii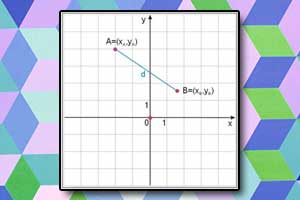
Odległość punktów
Półprosta
Łamana
Podstawowe pojęcia planimetrii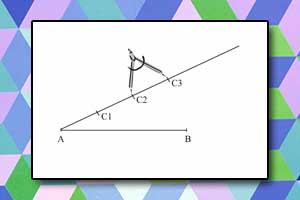
Podział odcinka© medianauka.pl, 2010-10-19, A-982
Data aktualizacji artykułu: 2023-05-22