Odległość między punktami
W niniejszym artykule omówimy pojęcie odległości punktów, odległości punktu od prostej i figury geometrycznej.
Odległość punktów
Aksjomat o odległości.
Każdym dwóm punktom \(A\) i \(B\) można przyporządkować liczbę, którą nazywamy odległością punktów.
Odległość oznaczamy następująco: \(|AB|\) lub \(|BA|\).
Odległość punktu od punktu musi spełniać łącznie następujące warunki:
- \(|AB|\) jest liczbą nieujemną.
- \(|AB|\) jest zerem wtedy i tylko wtedy, gdy \(A=B\).
- Jeśli trzy punkty \(A, B, C\) nie są współliniowe, to zachodzą jednocześnie następujące nierówności:
\(|AB|+|BC|>|AC|\) i \(|BC|+|CA|>|BA|\) i \(|CA|+|AB|>|CB|\).
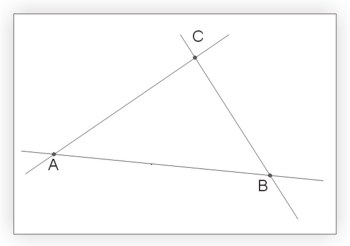
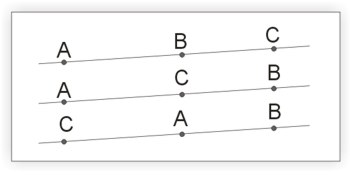
- Jeśli trzy punkty \(A, B, C\) są współliniowe, to zachodzi co najmniej jedna następujących równości: \(|AB|+|BC|=|AC| i |BC|+|CA|=|BA| i |CA|+|AB|=|CB|\).
Jednostka odległości
Wartość liczbowa odległości punktów zależy od tego, jaką odległość dwóch punktów przyjmiemy za jednostkę.
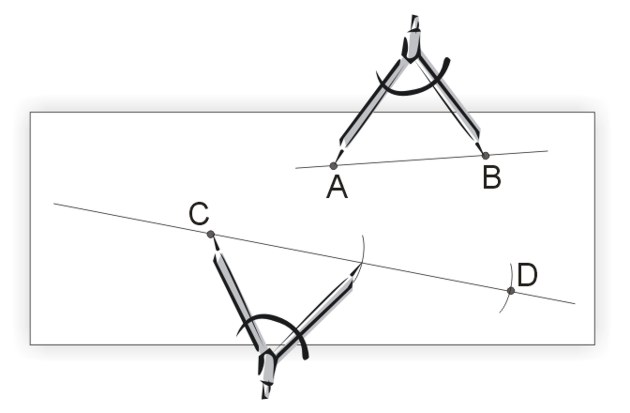
Jeżeli za jednostkę przyjmiemy odległość między dwoma punktami \(A\) i \(B\) (odległość między tymi punktami wynosi 1), to odległość punktów \(C\) i \(D\) wynosi 2, a sposób ich konstrukcji pokazano na powyższym rysunku.
Odległość między punktami w układzie współrzędnych
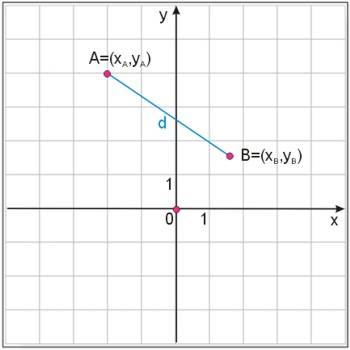
Odległość punktów \(A=(x_A,y_A), B=(x_B,y_B)\) obliczamy ze wzoru:
Wzór na odległość między punktami wynika bezpośrednio z twierdzenia Pitagorasa.
To tak zwana odległość euklidesowa.
Powyższy wzór w prosty sposób pozwala obliczyć odległość między dwoma punktami, gdy dane są jego współrzędne, co ilustrujemy poniższym przykładem.
Przykład
Dane są punkty: \(A=(1,2), B=(-1,4)\). Obliczyć odległość między tymi punktami.
Korzystamy z powyższego wzoru:
\(|AB|=\sqrt{(-1-1)^2+(4-2)^2}=\sqrt{4+4}=\sqrt{8}=2\sqrt{2}\)
Odległość punktu od prostej
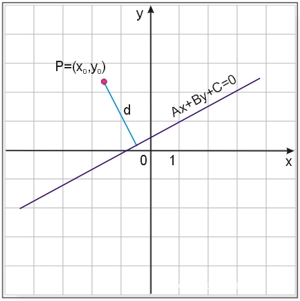
Wzór na odległość punktu od prostej
Odległość punktu \(P=(x_0,y_0)\) od prostej \(Ax+By+C=0\) wyrażona jest wzorem:
Zwykle nie mamy postaci prostej, jaka występuje we wzorze. Należy wówczas przekształcić (najczęściej) postać kierunkową prostej \(y=ax+b\) do postaci \(Ax+By+C=0\).
Powyższy wzór jest przydatny przy wyznaczaniu równań dwusiecznych kątów.
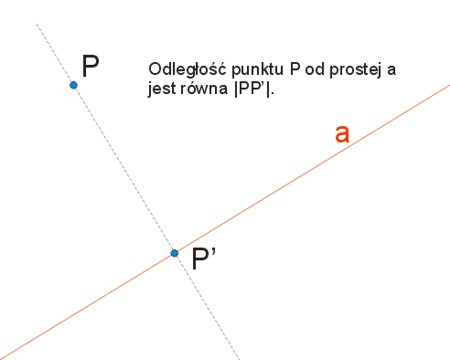
Odległość punktu od prostej równa jest odległości tego punktu od rzutu prostokątnego na tę prostą.
Odległość punktu od figury
Odległość punktu od niepustej figury jest to długość promienia największego otoczenia kołowego tego punktu, wewnątrz którego nie znajduje się żaden punkt ten figury.
Animacja
Zadania z rozwiązaniami
Zadanie nr 1.
Jaka jest odległość między różnymi punktami \(A, B\), jeżeli \(|AC|=4, |BC|=5\)?
Zadanie nr 2.
Obliczyć odległość początku układu współrzędnych od okręgu o równaniu \((x-3)^2+(y-3)^2=4\).
Zadanie nr 3.
Obliczyć odległość punktu \(A=(-3,4)\) od prostej o równaniu \(y=-2x+2\).
Zadanie nr 4.
Obliczyć odległość punktu \(M=(1,2)\) od trójkąta wyznaczonego przez punkty \(A=(-1,0), B=(5,-1), C=(1,-3)\).
Zadanie nr 5.
Znaleźć współrzędne punktów, których odległość od prostej \(y=3x+2\) jest równa \(\sqrt{2}\).
Zadanie nr 6.
Dane są punkty \(A=(\frac{\sqrt{2}}{2},2\sqrt{2}), \ B=(\frac{1}{\sqrt{2}}, 3\sqrt{2}+1)\). Obliczyć odległość \(|AB|\).
Zadanie nr 7.
Oblicz odległość punktu \(P=(3,2)\) od prostej \(3x+4y-1=0\).
Zadanie nr 9 — maturalne.
Odległość początku układu współrzędnych od prostej o równaniu \(y = 2x + 4\) jest równa
A. \(\frac{\sqrt{5}}{5}\)
B. \(\frac{4\sqrt{5}}{5}\)
C. \(\frac{4}{5}\)
D. \(4\)
Zadanie nr 10 — maturalne.
Punkt \(A=(7,−1)\) jest wierzchołkiem trójkąta równoramiennego \(ABC\), w którym \(|AC|=|BC|\). Obie współrzędne wierzchołka \(C\) są liczbami ujemnymi. Okrąg wpisany w trójkąt ABC ma równanie \(x^2+y^2=10\). Oblicz współrzędne wierzchołków \(B\) i \(C\) tego trójkąta.
Zadanie nr 11 — maturalne.
Prosta przechodząca przez punkty \(A=(8, −6)\) i \(B=(5, 15)\) jest styczna do okręgu o środku w punkcie \(O=(0, 0)\). Oblicz promień tego okręgu i współrzędne punktu styczności tego okręgu z prostą AB.
Zadanie nr 12 — maturalne.
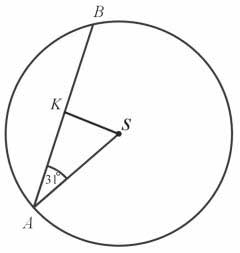W okręgu o środku w punkcie \(S\) poprowadzono cięciwę \(AB\), która utworzyła z promieniem \(AS\) kąt o mierze 31° (zobacz rysunek). Promień tego okręgu ma długość 10. Odległość punktu \(S\) od cięciwy \(AB\) jest liczbą z przedziału
A. \(\langle \frac{9}{2};\frac{11}{2}\rangle\)
B. \(\langle \frac{11}{2};\frac{13}{2}\rangle\)
C. \(\langle \frac{13}{2};\frac{19}{2}\rangle\)
D. \(\langle \frac{19}{2};\frac{37}{2}\rangle\)
Inne zagadnienia z tej lekcji
Aksjomaty planimetrii
Półprosta
Odcinek
Łamana
Podstawowe pojęcia planimetrii© medianauka.pl, 2010-10-10, A-974
Data aktualizacji artykułu: 2023-05-21