Nauka » Matematyka » Odległość punktów

Zadanie - odległość punktów

Jaka jest odległość między różnymi punktami A, B, jeżeli |AC|=4, |BC|=5?

Rozwiązanie zadania uproszczone

1) |AB|>0
2) Gdy punkty są współliniowe:
|AB|+|BC|=|AC|
|AB|+5=4
|AB|=1
|AB|+|AC|=|BC|
|AB|+4=5
|AB|=-1 - nie spełnia warunku 1
|AC|+|BC|=|AB|
4+5=|AB|
|AB|=9
3)Gdy punkty nie są współliniowe:
$\begin{cases} |AB|+|BC|>|AC|\\ |AB|+|AC|>|BC|\\ |AC|+|BC|>|AB|\end{cases}\\ \begin{cases} |AB|+5>4\\ |AB|+4>5\\ 4+5>|AB|\end{cases}\\ \begin{cases} |AB|>-1\\ |AB|>1\\ |AB|<9 \end{cases} \\ |AB|\in <1;9>$

Rozwiązanie zadania ze szczegółowymi wyjaśnieniami

Posługujemy się aksjomatem o odległości. Odległość jest nieujemna, więc:

1) |AB|>0

Teraz rozpatrzymy przypadek, gdy punkty są współliniowe. Musi być więc spełniony jeden z warunków: |AB|+|BC|=|AC| i |BC|+|CA|=|BA| i |CA|+|AB|=|CB|. Podstawiamy więc wartości liczbowe i wyznaczamy z równań |AB|

|AB|+|BC|=|AC|
|AB|+5=4
|AB|=1

|AB|+|AC|=|BC|
|AB|+4=5
|AB|=-1 - nie spełnia warunku 1, więc rozwiązania nie bierzemy pod uwagę.

|AC|+|BC|=|AB|
4+5=|AB|
|AB|=9

Zatem
|AB|=1 lub |AB|=9

2) Teraz sprawdzimy przypadek, gdy punkty nie są współliniowe. Spełnione (zgodnie z aksjomatem odległości) muszą być wszystkie trzy nierówności:

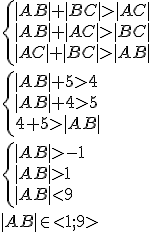
$\begin{cases} |AB|+|BC|>|AC|\\ |AB|+|AC|>|BC|\\ |AC|+|BC|>|AB|\end{cases}\\ \begin{cases} |AB|+5>4\\ |AB|+4>5\\ 4+5>|AB|\end{cases}\\ \begin{cases} |AB|>-1\\ |AB|>1\\ |AB|<9 \end{cases} \\ |AB|\in <1;9>$

Warto zaznaczyć przedziały na osi liczbowej i znaleźć część wspólną, uwzględniając warunki 1 i 2

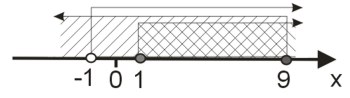
otrzymujemy rozwiązanie: $|AB|\in <1;9>$

Odpowiedź

$|AB|\in <1;9>$

Zadania podobne

Zadanie - odległość punktów
Sprawdzić, czy istnieją takie punkty A, B i C, że
a) |AB|=10, |AC|=5, |BC|=5
b) |AB|=10, |AC|=4, |BC|=5
c) |AB|=10, |AC|=6, |BC|=5

Pokaż rozwiązanie zadania

Zadanie - odległość początku układu współrzędnych od okręgu
Obliczyć odległość początku układu współrzędnych od okręgu o równaniu (x-3)²+(y-3)²=4

Pokaż rozwiązanie zadania

Zadanie - odległość punktu od prostej
Obliczyć odległość punktu A=(-3,4) od prostej o równaniu

Pokaż rozwiązanie zadania

Zadanie - odległość punktu od figury
Obliczyć odległość punktu M=(1,2) od trójkąta wyznaczonego przez punkty A=(-1,0), B=(5,-1), C=(1,-3)

Pokaż rozwiązanie zadania

Zadanie - odległość punktu od prostej
Znaleźć współrzędne punktów, których odległość od prostej y=3x+2 jest równa $\sqrt{2}$

Pokaż rozwiązanie zadania

Zadanie - odległość punktów
Dane są punkty $A=(\frac{\sqrt{2}}{2},2\sqrt{2}), \ B=(\frac{1}{\sqrt{2}}, 3\sqrt{2}+1)$ . Obliczyć odległość |AB|.

Pokaż rozwiązanie zadania

Zadanie - odległość punktu od prostej
Oblicz odległość punktu P=(3,2) od prostej 3x+4y-1=0.

Pokaż rozwiązanie zadania

Zadanie - odległość punktu od prostej
Oblicz odległość punktu P=(-1,1) od prostej y=2x-1.

Pokaż rozwiązanie zadania

Zadanie maturalne nr 13, matura 2016 (poziom podstawowy)
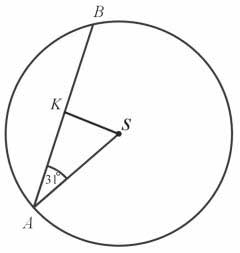ilustracja do zadania 13 , matura 2016

W okręgu o środku w punkcie S poprowadzono cięciwę AB, która utworzyła z promieniem AS kąt o mierze 31° (zobacz rysunek). Promień tego okręgu ma długość 10. Odległość punktu S od cięciwy AB jest liczbą z przedziału

A.

Pokaż rozwiązanie zadania

Zadanie maturalne nr 5, matura 2015 (poziom rozszerzony)
Odległość początku układu współrzędnych od prostej o równaniu y = 2x + 4 jest równa

A. $\frac{\sqrt{5}}{5}$
B. $\frac{4\sqrt{5}}{5}$
C. $\frac{4}{5}$
D. 4

Pokaż rozwiązanie zadania

Zadanie maturalne nr 10, matura 2018 (poziom rozszerzony)

Punkt A=(7,−1) jest wierzchołkiem trójkąta równoramiennego ABC, w którym |AC|=|BC|. Obie współrzędne wierzchołka C są liczbami ujemnymi. Okrąg wpisany w trójkąt ABC ma równanie x²+y²=10. Oblicz współrzędne wierzchołków B i C tego trójkąta.

Pokaż rozwiązanie zadania

Niektóre treści nie są dostosowane do Twojego profilu. Jeżeli jesteś pełnoletni możesz wyrazić zgodę na przetwarzanie swoich danych osobowych. W ten sposób będziesz miał także wpływ na rozwój naszego serwisu.