Nauka » Matematyka » Odległość punktów

Zadanie - odległość punktu od figury

Obliczyć odległość punktu M=(1,2) od trójkąta wyznaczonego przez punkty A=(-1,0), B=(5,-1), C=(1,-3)

Rozwiązanie zadania uproszczone

Szukane:|MN|.

1) Szukamy równania prostej y=a₁x+b₁, wyznaczonej przez A, B

$\underline{ - \ \ \ \begin{cases} 0=-a_1+b_1\\ -1=5a_1+b_1\end{cases}}\\ 1=-6a_1/:(-6)\\a_1=-\frac{1}{6}\\ b_1=-\frac{1}{6}\\ y=-\frac{1}{6}x-\frac{1}{6}$

2) Szukamy równania prostej y=a₂x+b₂.
$a_2=-\frac{1}{-\frac{1}{6}}=6\\ y=6x+b_2$
$2=6+b_2\\ b_2=-4\\ y=6x-4$

3) Szukamy współrzędnych punktu N.

$\begin{cases}y=-\frac{1}{6}x-\frac{1}{6}\\ y=6x-4\end{cases} \\ -6x-4=-\frac{1}{6}x-\frac{1}{6}/\cdot 6\\ 36x-24=-x-1\\ 35x=23/:35\\ x=\frac{23}{35}\\ y=6x-4\\ y=6\cdot \frac{23}{37}-4\\ y=-\frac{10}{37}$
$|MN|=\sqrt{(\frac{23}{37}-1)^2+(-\frac{10}{37}-2)^2}=2\frac{11}{37}$

Rozwiązanie zadania ze szczegółowymi wyjaśnieniami

Odległość punktu od niepustej figury jest to długość promienia największego otoczenia kołowego tego punktu, wewnątrz którego nie znajduje się żaden punkt ten figury. Sporządzamy rysunek.

Otoczenie punktu M, o którym mowa jest zaznaczone na niebiesko (okrąg). Szukamy odległości |MN|. Aby to uczynić, musimy znaleźć współrzędne punktu B.

Punkt N jest punktem przecięcia się prostej wyznaczonej przez punkty A, B (oznaczmy równanie tej prostej przez y=a₁x+b₁) i prostej prostopadłej do niej, przechodzącej przez punkt N. Prostą tę oznaczamy następująco: y=a₂x+b₂. Musimy znaleźć współczynniki a i b obu prostych

1) Szukamy równania prostej y=a₁x+b₁

Wiemy, że prosta przechodzi przez punkty A=(-1,0) oraz B=5,-1. Podstawiamy do równania prostej współrzędne tych punktów i rozwiązujemy układ równań:

$y=a_1x+b_1\\ \begin{cases} 0=a_1\cdot (-1)+b_1\\ -1=a_1\cdot 5+b_1\end{cases} \\ \underline{ - \ \ \ \begin{cases} 0=-a_1+b_1\\ -1=5a_1+b_1\end{cases}}\\ 1=-6a_1/:(-6)\\a_1=-\frac{1}{6}\\ 0=-a_1+b_1\\ a_1=b_1\\ b_1=-\frac{1}{6}\\ y=-\frac{1}{6}x-\frac{1}{6}$

2) Szukamy równania prostej y=a₂x+b₂. Skorzystamy z własności prostych prostopadłych. Ich współczynniki kierunkowe spełniają warunek:

$a_1=-\frac{1}{a_2}$

Mamy więc:

$a_2=-\frac{1}{-\frac{1}{6}}=6\\ y=6x+b_2$

Wiemy, że prosta przechodzi przez punkt M=(1,2). Podstawiamy do równania prostej współrzędne punktu i rozwiązujemy równanie:

$2=6\cdot 1+b_2\\ 2-6=b_2\\ b_2=-4\\ y=6x-4$

3) Szukamy współrzędnych punktu N. Punkt ten jest miejscem przecięcia się wyznaczonych wyżej prostych. Wystarczy więc rozwiązać układ równań:

Otrzymaliśmy więc współrzędne punktu N. Możemy już obliczyć odległość |MN|

Skorzystamy ze wzoru na odległość punktów w układzie współrzędnych:

$z=\sqrt{(x_B-x_A)^2+(y_B-y_A)^2}$

Obliczamy odległość między punktami o współrzędnych: $M=(1,2), N=(\frac{23}{37}, -\frac{10}{37})$ . Korzystamy z powyższego wzoru:

$|MN|=\sqrt{(\frac{23}{37}-1)^2+(-\frac{10}{37}-2)^2}=\sqrt{(\frac{13}{37})^2+(\frac{84}{37})^2}=\sqrt{\frac{169+7036}{37}}=\frac{\sqrt{7225}}{37}=\frac{85}{37}=2\frac{11}{37}$

Odpowiedź

$|MN|=2\frac{11}{37}$

Zadania podobne

Zadanie - odległość punktów
Sprawdzić, czy istnieją takie punkty A, B i C, że
a) |AB|=10, |AC|=5, |BC|=5
b) |AB|=10, |AC|=4, |BC|=5
c) |AB|=10, |AC|=6, |BC|=5

Pokaż rozwiązanie zadania

Zadanie - odległość punktów
Jaka jest odległość między różnymi punktami A, B, jeżeli |AC|=4, |BC|=5?

Pokaż rozwiązanie zadania

Zadanie - odległość początku układu współrzędnych od okręgu
Obliczyć odległość początku układu współrzędnych od okręgu o równaniu (x-3)²+(y-3)²=4

Pokaż rozwiązanie zadania

Zadanie - odległość punktu od prostej
Obliczyć odległość punktu A=(-3,4) od prostej o równaniu

Pokaż rozwiązanie zadania

Zadanie - odległość punktu od prostej
Znaleźć współrzędne punktów, których odległość od prostej y=3x+2 jest równa $\sqrt{2}$

Pokaż rozwiązanie zadania

Zadanie - odległość punktów
Dane są punkty $A=(\frac{\sqrt{2}}{2},2\sqrt{2}), \ B=(\frac{1}{\sqrt{2}}, 3\sqrt{2}+1)$ . Obliczyć odległość |AB|.

Pokaż rozwiązanie zadania

Zadanie - odległość punktu od prostej
Oblicz odległość punktu P=(3,2) od prostej 3x+4y-1=0.

Pokaż rozwiązanie zadania

Zadanie - odległość punktu od prostej
Oblicz odległość punktu P=(-1,1) od prostej y=2x-1.

Pokaż rozwiązanie zadania

Zadanie maturalne nr 13, matura 2016 (poziom podstawowy)
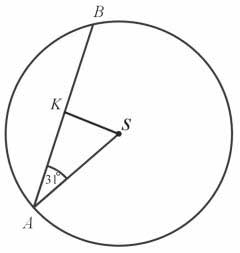ilustracja do zadania 13 , matura 2016

W okręgu o środku w punkcie S poprowadzono cięciwę AB, która utworzyła z promieniem AS kąt o mierze 31° (zobacz rysunek). Promień tego okręgu ma długość 10. Odległość punktu S od cięciwy AB jest liczbą z przedziału

A.

Pokaż rozwiązanie zadania

Zadanie maturalne nr 5, matura 2015 (poziom rozszerzony)
Odległość początku układu współrzędnych od prostej o równaniu y = 2x + 4 jest równa

A. $\frac{\sqrt{5}}{5}$
B. $\frac{4\sqrt{5}}{5}$
C. $\frac{4}{5}$
D. 4

Pokaż rozwiązanie zadania

Zadanie maturalne nr 10, matura 2018 (poziom rozszerzony)

Punkt A=(7,−1) jest wierzchołkiem trójkąta równoramiennego ABC, w którym |AC|=|BC|. Obie współrzędne wierzchołka C są liczbami ujemnymi. Okrąg wpisany w trójkąt ABC ma równanie x²+y²=10. Oblicz współrzędne wierzchołków B i C tego trójkąta.

Pokaż rozwiązanie zadania

Niektóre treści nie są dostosowane do Twojego profilu. Jeżeli jesteś pełnoletni możesz wyrazić zgodę na przetwarzanie swoich danych osobowych. W ten sposób będziesz miał także wpływ na rozwój naszego serwisu.