Łamana

łamana

Definicja

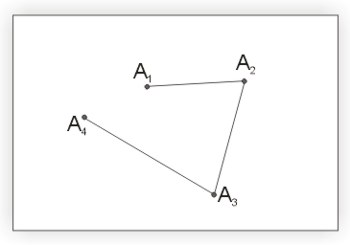
Rozpatrujemy ciąg punktów \(A_1,A_2,A_3,...,A_n\), gdzie \(n\) — dowolna liczna naturalna większa od dwóch. Tworzymy łańcuch odcinków, łącząc każde dwa kolejne punkty tego ciągu odcinkami: \(\overline{A_1A_2},\overline{A_2A_3},...,\overline{A_{n-1}A_n}\). Łamana jest to figura utworzona z tak skonstruowanych odcinków, jeżeli każde dwa odcinki tego łańcucha mają co najwyżej jeden punkt wspólny.

Każdy z punktów \(A_1,A_2,A_3,...,A_n\) nazywamy wierzchołkiem, a każdy z odcinków łączących kolejne punkty nazywamy bokami łamanej.

Na poniższym rysunku pokazano przykłady łamanych:

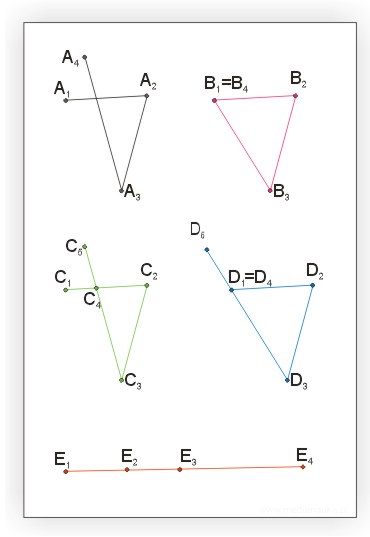
łamane

Wszystkie przedstawione figury są przykładami łamanej, mimo tego, że niektóre punkty się pokrywają, odcinki przecinają lub są współliniowe.

Łamana zwyczajna

Jeżeli:

dwa odcinki, które mają wspólny koniec, nie leżą na jednej prostej,
dwa odcinki, niemające wspólnego końca, nie mają wspólnego punktu,
każdy z wierzchołków jest końcem co najwyżej dwóch odcinków,

to łamaną nazywamy łamaną zwyczajną.

Na przedstawionym obok rysunku tylko łamana \(B_1, B_2, B_3, B_4\) jest łamaną zwyczajną (łamaną zwyczajną jest również łamana pokazana na rysunku obok definicji łamanej).

Łamana zamknięta i łamana otwarta

Łamana może być zamknięta, gdy \(A_1=A_n\), lub otwarta, gdy ten warunek nie jest spełniony.

Na rysunku obok tylko łamana\(B_1, B_2, B_3, B_4\) jest zamknięta. Pozostałe są łamanymi otwartymi.

Powiązane materiały

Aksjomaty planimetrii

Odległość punktów

Półprosta

Odcinek

Podstawowe pojęcia planimetrii