Układ współrzędnych
Aby podać interpretację geometryczną funkcji, korzystamy z pojęcia układu współrzędnych.
Definicja
Układ współrzędnych prostokątnych (kartezjański układ współrzędnych) na płaszczyźnie jest to para osi liczbowych prostopadłych do siebie, o wspólnym początku O.
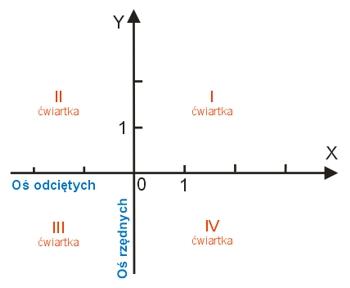
Oś pozioma to oś odciętych. Oznaczamy ją przez OX.
Oś pionowa to oś rzędnych. Oznaczamy ją przez OY.
Prostokątny układ współrzędnych dzieli płaszczyznę na cztery ćwiartki, które numerujemy tak, jak to ilustruje powyższy rysunek.
Na osi odciętych odkładamy wartości zmiennych niezależnych \(x\), na osi rzędnych odkładamy wartości zmiennej zależnej funkcji \(y\).
Kartezjański układ współrzędnych w przestrzeni określa się analogicznie. Wszystkie trzy osie tego układu są do siebie prostopadłe.
Współrzędne punktu
Każdemu punktowi na płaszczyźnie w układzie współrzędnych można przyporządkować parę liczb \((x,y)\):
- x — odcięta — współrzędna na osi OX rzutu prostokątnego punktu na tę oś,
- y — rzędna — współrzędna na osi OY rzutu prostokątnego punktu na tę oś,
które nazywamy współrzędnymi punktu.
Współrzędne punktu A oznaczamy w następujący sposób: \(A(x,y)\) lub \(A=(x,y)\).
- Początek układu OXY ma współrzędne \(O(0,0)\).
- Każdy punkt na osi OX ma współrzędne \((x,0)\).
- Każdy punkt na osi OY ma współrzędne \((0,y)\).
Przykład
Na poniższej ilustracji zaznaczono w układzie współrzędnych kilka przykładowych punktów wraz z określeniem ich współrzędnych.
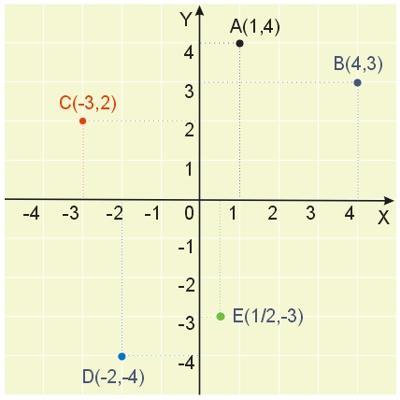
Pytania
Czy są inne układy współrzędnych?
Tak. Stosuje się także w matematyce i innych naukach:
- układ współrzędnych biegunowych,
- układ współrzędnych walcowych,
- układ współrzędnych sferycznych.
Powiązane materiały
Oś liczbowa
Wykres funkcji
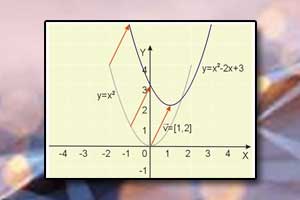Przesunięcie wykresu funkcji
Pomocniczy układ współrzędnych
Wykres funkcji jednej zmiennej
Prostokątny układ współrzędnych
Układ współrzędnych — quiz© medianauka.pl, 2009-05-03, A-197
Data aktualizacji artykułu: 2023-04-06