Parabola — wykres funkcji kwadratowej
Wykresem funkcji kwadratowej jest parabola.
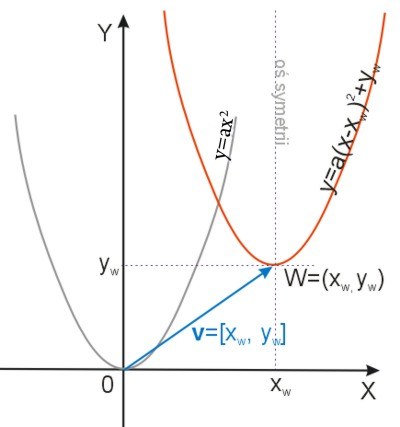
Jak wynika z postaci kanonicznej trójmianu kwadratowego, a także z przesunięcia wykresu funkcji w układzie współrzędnych, wykres funkcji:
\(y=ax^2+bx+c=a(x+\frac{b}{2a})^2-\frac{\Delta}{4a}=a(x-x_w)^2+y_w\)
jest parabolą, która powstaje w wyniku przesunięcia wykresu funkcji \(y=ax^2\) o wektor \(\vec{v}=[x_w,y_w]\), przy czym \(x_w=-\frac{b}{2a},\quad{y_w}=-\frac{\Delta}{4a}\).
W przypadku dodatniego współczynnika \(a\) mamy:
Wykres funkcji
Poniższa aplikacja pokazuje zachowanie się wykresu funkcji kwadratowej w zależności od wartości współczynników a, b oraz c.
Funkcja w postaci y = ax+b, czyli y = x
a 1b 0
c 0
Wyróżnik trójmianu kwadratowego Δ=0
Istnieje jedno miejsce zerowe.
Współrzędne wierzchołka paraboli:
Wykresy funkcji kwadratowej — wszystkie przypadki
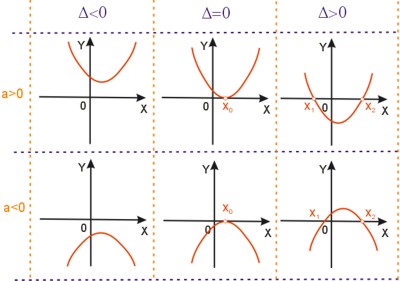
Wszystkie możliwości zmienności wykresu trójmianu kwadratowego, w zależności od współczynnika \(a\) oraz wyróżnika trójmianu kwadratowego, zostały pokazane na poniższym schemacie.
Cechy wykresu i funkcji kwadratowej
- Wykresem funkcji kwadratowej jest parabola.
- Ramiona paraboli skierowane są w górę, jeżeli \(a>0\), w dół w przypadku gdy \(a<0\).
- Współrzędne wierzchołka paraboli: \(W(-\frac{b}{2a},-\frac{\Delta}{4a})\).
- Wykres funkcji kwadratowej nie ma miejsc zerowych, jeżeli \(\Delta>0\).
- Wykres funkcji kwadratowej ma jedno miejsce zerowe równe \(x_0=-\frac{b}{2a}\), jeżeli \(\Delta=0\).
- Wykres funkcji kwadratowej ma dwa miejsca zerowe równe \(x_1=\frac{-b-sqrt{\Delta}}{2a},\quad{x_2}=\frac{-b+sqrt{\Delta}}{2a}\), jeżeli \(\Delta>0\).
- Parabola ma jedną oś symetrii o równaniu \(x=-\frac{b}{2a}\).
- Funkcja przyjmuje minimum dla \(a>0\) w punkcie \(x=-\frac{b}{2a}\) równe \(y=-\frac{\Delta}{4a}\).
- Funkcja przyjmuje maksimum dla \(a<0\) w punkcie \(x=-\frac{b}{2a}\) równe \(y=-\frac{\Delta}{4a}\).
- Gdy \(a>0\) funkcja maleje w przedziale \(x\in (-\infty;-\frac{b}{2a})\) i rośnie w przedziale \(y\in (-\frac{b}{2a};+\infty)\).
- Gdy \(a<0\) funkcja rośnie w przedziale \(x\in (-\infty;-\frac{b}{2a})\) i maleje w przedziale \(y\in (-\frac{b}{2a};+\infty)\).
Jak narysować parabolę?
Parabola jest krzywą, więc do jej wyznaczenia potrzeba minimum trzech punktów. Zwykle są to miejsca zerowe funkcji oraz wierzchołek. W przypadku, gdy funkcja nie posiada miejsc zerowych wystarczy znaleźć punkt przecięcia się wykresu z osią OY i skorzystać z osi symetrii wykresu.
Przykłady
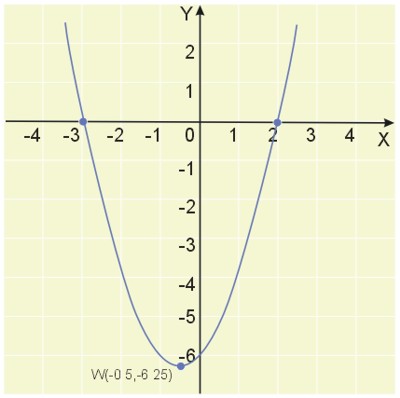
Naszkicować wykres funkcji \(y=x^2+x-6\).
Mamy więc:
\(a=1, b=1, c=-6\)
Obliczamy wyróżnik trójmianu kwadratowego:
\(\Delta=b^2-4ac=1^2-4\cdot{1}\cdot{(-6)=25}\)
\(\sqrt{\Delta}=5\)
Wyróżnik jest dodatni, więc funkcja ma dwa miejsca zerowe.
\(x_1=\frac{-b-\sqrt{\Delta}}{2a}=\frac{-1-5}{2}=-3\)
\({x_2=\frac{-b+\sqrt{\Delta}}{2a}=\frac{-1+5}{2}=2}\)
Znajdźmy jeszcze współrzędne wierzchołka.
Możemy obliczyć je, wstawiając wartości liczbowe do wzoru \(W(-\frac{b}{2a},-\frac{\Delta}{4a})\).
Jednak my sprowadzimy funkcję do postaci kanonicznej. Nie zawsze bowiem pamiętamy wzory!
\(y=x^2+x-6\)
\(y=x^2+2\cdot{\frac{1}{2}}x+\frac{1}{4}-\frac{1}{4}-6\)
\({y=(x+\frac{1}{2})^2-6\frac{1}{4}}\)
Zatem współrzędne wierzchołka to \((-\frac{1}{2},-6\frac{1}{4})\).
Wiedząc, że współczynnik \(a>0\) wiemy, że ramiona paraboli są skierowane ku górze, łatwo naszkicujemy wykres tej funkcji.
Pytania
Jak naszkicować wykres funkcji kwadratowej?
Parabolę wyjątkowo często trzeba szkicować w kursie matematyki. Nie zawsze trzeba wykonywać dokładny wykres, często wystarczy zaznaczenie jedynie kilku istotnych cech paraboli. Poniżej kilka porad:
- Jeżeli współczynnik \(a\) przy \(x^2\) jest dodatni, to ramiona paraboli są skierowane ku górze, w przeciwnym przypadku — w dół.
- Jeżeli Δ>0 — obliczamy dwa miejsca zerowe, jeżeli Δ=0 — mamy tylko jedno miejsce zerowe, jeżeli zaś Δ jest ujemne, funkcja nie posiada miejsc zerowych (nie przecina osi OX).
- Do naszkicowania paraboli są potrzebne minimum 3 punkty: znajdujemy współrzędne wierzchołka i pierwiastki lub dowolne inne punkty (na przykład punkt przecięcia paraboli z osi OY — wstawiając za \(x\) do wzoru funkcji liczbę 0).
Ćwiczenia
Ćwiczenia interakcyjne pomogą przygotować się na sprawdzian, test, egzamin, a ponadto usystematyzują wiedzę z danej dziedziny. To także świetny trening do matury. Wiele ćwiczeń to dobre zadania maturalne.
Zadania z rozwiązaniami
Zadanie nr 2.
Dla jakiej wartości parametrów \(m\) i \(n\) wierzchołkiem paraboli o równaniu \(y=x^2-mx+n+1\) jest punkt \(A(2,1)\)?
.Zadanie nr 5.
Znaleźć równanie osi symetrii paraboli o równaniu \(f(x)=-2x^2+x-3\).
Zadanie nr 6.
Sporządzić wykres funkcji \(f(x)=\begin{cases}x^2 \ dla \ x<0\\ -x^2\ dla \ x\geq 0\end{cases}\)
Zadanie nr 7.
Znaleźć równanie paraboli, której fragment przedstawiono na rysunku:
Zadanie nr 8 — maturalne.
Na rysunku przedstawiony jest fragment paraboli będącej wykresem funkcji kwadratowej \(f\). Wierzchołkiem tej paraboli jest punkt \(W=(1,9)\). Liczby \(-2\) i \(4\) to miejsca zerowe funkcji \(f\).
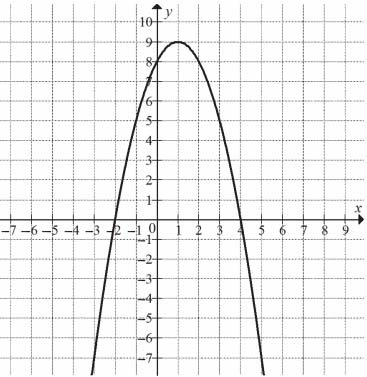
Zbiorem wartości funkcji \(f\) jest przedział:
A. \((-\infty,-2]\)
B. \([-2,4]\)
C. \([4,\infty)\)
Zadanie nr 9 — maturalne.
Na rysunku przedstawiony jest fragment paraboli będącej wykresem funkcji kwadratowej \(f\). Wierzchołkiem tej paraboli jest punkt \(W=(1,9)\). Liczby \(-2\) i \(4\) to miejsca zerowe funkcji \(f\).
Najmniejsza wartość funkcji \(f\) w przedziale \([−1, 2]\) jest równa
A. \(2\)
B. \(5\)
C. \(8\)
D. \(9\)
Zadanie nr 10 — maturalne.
Wykresem funkcji kwadratowej \(f(x)=2x^2+bx+c\) jest parabola, której wierzchołkiem jest punkt \(W=(4,0)\). Oblicz wartości współczynników \(b\) i \(c\).
Zadanie nr 11 — maturalne.
Wykresem funkcji kwadratowej \(f(x)=x^2−6x−3\) jest parabola, której wierzchołkiem jest punkt o współrzędnych
- \((-6,-3)\)
- \((-6,69)\)
- \((3,-12)\)
- \((6,-3)\)
Zadanie nr 12 — maturalne.
Na rysunku przedstawiony jest fragment paraboli będącej wykresem funkcji kwadratowej \(f\). Wierzchołkiem tej paraboli jest punkt \(W=(2,− 4)\). Liczby \(0\) i \(4\) to miejsca zerowe funkcji \(f\).
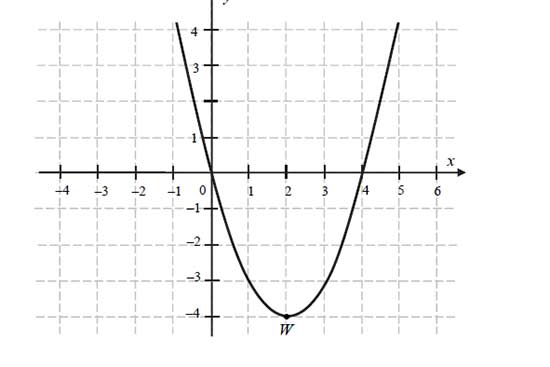
Zadanie 8: Zbiorem wartości funkcji \(f\) jest przedział
A. \((-\infty ,0\rangle \)
B. \(\langle 0, 4\rangle \)
C. \(\langle -4, +\infty)\)
D. \(\langle 4, +\infty)\)
Zadanie 9: Największa wartość funkcji \(f\) w przedziale \(\langle 1, 4\rangle \) jest równa
A. \(-3\)
B. \(-4\)
C. \(4\)
D. \(0\)
Zadanie 10: Osią symetrii wykresu funkcji \(f\) jest prosta o równaniu
A. \(x=-4\)
B. \(x=-4\)
C. \(y=2\)
D. \(x=2\)
Zadanie nr 13 — maturalne.
Funkcja kwadratowa \(f\) jest określona wzorem \(f(x)=a(x−1)(x−3)\). Na rysunku przedstawiono fragment paraboli będącej wykresem tej funkcji. Wierzchołkiem tej paraboli jest punkt \(W=(2,1)\).
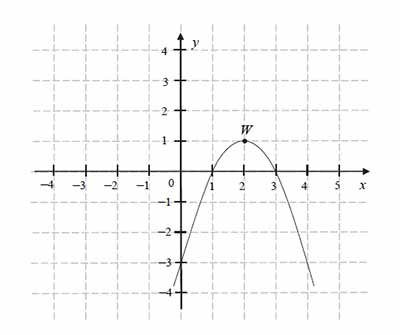
Współczynnik a we wzorze funkcji \(f\) jest równy
A. \(1\)
B. \(2\)
C. \(-2\)
D. \(-1\)
Największa wartość funkcji \(f\) w przedziale \(\langle 1, 4\rangle \) jest równa
A. \(-3\)
B. \(0\)
C. \(1\)
D. \(2\)
Osią symetrii paraboli będącej wykresem funkcji \(f\) jest prosta o równaniu
A. \(x=1\)
B. \(x=2\)
C. \(y=1\)
D. \(y=2\)
Zadanie nr 14 — maturalne.
Funkcja kwadratowa \(f\) określona wzorem \(f(x)=-2(x+1)(x-3)\) jest malejąca w przedziale
A. \([1, +\infty)\)
B. \((−\infty, 1]\)
C. \((−\infty, −8]\)
D. \([−8, +\infty)\)
Zadanie nr 15 — maturalne.
Jednym z miejsc zerowych funkcji kwadratowej \(f\) jest liczba \((−5)\). Pierwsza współrzędna wierzchołka paraboli, będącej wykresem funkcji \(f\), jest równa \(3\). Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. Drugim miejscem zerowym funkcji \(f\) jest liczba
A. 11
B. 1
C. (-1)
D. (-13)
Inne zagadnienia z tej lekcji
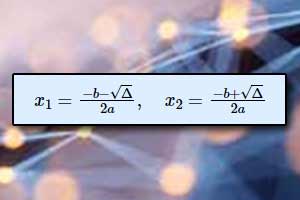Miejsca zerowe funkcji kwadratowej
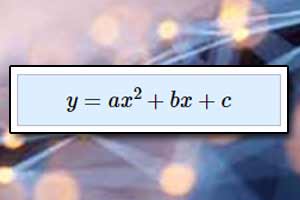Funkcja kwadratowa
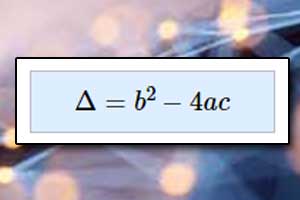Postać kanoniczna funkcji kwadratowej
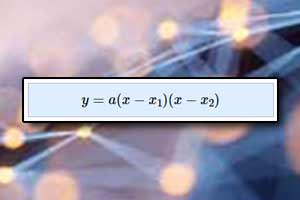Postać iloczynowa trójmianu kwadratowego
Właściwości i wykres funkcji kwadratowej© medianauka.pl, 2009-07-20, A-270
Data aktualizacji artykułu: 2023-04-22