Postać iloczynowa funkcji kwadratowej
Trójmian kwadratowy \(y=ax^2+bx+c\) można rozłożyć na czynniki liniowe. Jest to możliwe w przypadku, gdy \(\Delta\geq{0}\). Wówczas wzór na postać iloczynową funkcji drugiego stopnia jest następujący:
gdzie:
Przypomnijmy, że
jest to wyróżnik trójmianu kwadratowego
Liczby \(x_1\) oraz \(x_2\) są punktami zerowymi (pierwiastkami) trójmianu kwadratowego.
W szczególnym przypadku, gdy \(\Delta=0\) oba pierwiastki są sobie równe (\(x_1=x_2=\frac{-b}{2a}=x_0\)) i postać iloczynową trójmianu kwadratowego można zapisać w następujący sposób:
W przypadku, gdy \(\Delta<0\) trójmian kwadratowy nie ma postaci iloczynowej.
Podsumowanie
Postać iloczynowa trójmianu kwadratowego jest zatem następująca:
Gdy \(\Delta >0\) funkcja kwadratowa ma dwa miejsca zerowe:
\(x_1=\frac{-b-\sqrt{\Delta}}{2a},\quad{x_2=\frac{-b+\sqrt{\Delta}}{2a}}\)
Gdy \(\Delta=0\) funkcja kwadratowa ma jedno miejsce zerowe:
\(x_0=\frac{-b}{2a}\)
Gdy \(\Delta<0\) funkcja kwadratowa nie ma miejsc zerowych.
Przykłady
Przedstaw trójmian kwadratowy w postaci iloczynowej: \(f(x)=3x^2-12x-15\).
Mamy tutaj:
\(a=3, b=-12, c=-15\)
Więc:
\(\Delta=b^2-4ac=(-12)^2-4\cdot{3}\cdot{(-15)}=144+180=324\)
Wyróżnik kwadratowy jest większy od zera, więc funkcja ma dwa miejsca zerowe.
\(\sqrt{\Delta}=\sqrt{324}=18\)
\(x_1=\frac{-b-\sqrt{\Delta}}{2a}=\frac{12-18}{6}=-1\)
\({x_2=\frac{-b+\sqrt{\Delta}}{2a}=\frac{12+18}{6}=\frac{30}{6}=5}\)
Mamy więc postać iloczynową:
\(f(x)=a(x-x_1)(x-x_2)=3(x+1)(x-5)\)
Wyprowadzenie postaci iloczynowej funkcji kwadratowej
Aby otrzymać postać iloczynową trójmianu kwadratowego, wystarczy postać kanoniczną sprowadzić do wzoru skróconego mnożenia \(A^2-B^2=(A-B)(A+B)\). Czynnik \(A^2\) został podkreślony w postaci kanonicznej trójmianu. Brakuje czynnika \(B^2\).
\(y=a(x+\frac{b}{2a})^2-\frac{\Delta}{4a}= a[\underline{(x+\frac{b}{2a})^2}-\frac{\Delta}{4a^2}]\)
Jeżeli założymy, że \(\Delta\geq{0}\) możemy napisać, że \(B=(\frac{\sqrt{\Delta}}{2a})^2,\quad{B^2} =\frac{\Delta}{4a^2}\). Mamy więc czynnik \(B^2\) (w naszym wzorze został podkreślony).
\(y=a[(x+\frac{b}{2a})^2-\underline{(\frac{\sqrt{\Delta}}{2a})^2}]\)
Możemy więc skorzystać ze wspomnianego wyżej wzoru skróconego mnożenia i otrzymujemy wówczas wzór:
\(y=a(x+\frac{b}{2a}+\frac{\sqrt{\Delta}}{2a})(x+\frac{b}{2a}-\frac{\sqrt{\Delta}}{2a})=a(x-\frac{-b-\sqrt{\Delta}}{2a})(x-\frac{-b+\sqrt{\Delta}}{2a})\)
Stosując odpowiednie oznaczenia mamy:
\(y=a(x-x_1)(x-x_2)\)
Gdy \(\Delta=0,\quad{\sqrt{\Delta}}=0\) i powyższy wzór przyjmuje postać:
\(y=a(x-\frac{-b-0}{2a})(x-\frac{-b+0}{2a})=a(x-\frac{-b}{2a})^2=a(x-x_0)^2\)
Pytania
Co to jest trójmian kwadratowy?
Jest to nazwa funkcji kwadratowej, która jest szczególnym przypadkiem wielomianu. Sama nazwa „trójmian” oznacza, że funkcja ta składa się z trzech składników, a słowo „kwadratowy” wskazuje na stopień wielomianu, czyli największą potęgę, w jakiej występuje zmienna.
Czy funkcję kwadratową można zawsze wyrazić w postaci iloczynowej?
Nie. Jest to możliwe tylko w przypadku, gdy \(\Delta\geq 0\).
Zadania z rozwiązaniami

Zadanie nr 1.
Przedstawić funkcję
a) \(f(x)=-x^2+7x-12\)
b) \(f(x)=2x^2+44x+242\)
w postaci iloczynowej.

Zadanie nr 2.
Zapisać wzór funkcji kwadratowej, która ma dwa miejsca zerowe \(x_1=-1\) oraz \(x_2=5\), wiedząc że parabola przecina oś OY w punkcie (0,15).

Zadanie nr 3 — maturalne.
Na rysunku przedstawiono fragment wykresu funkcji kwadratowej \(f\).
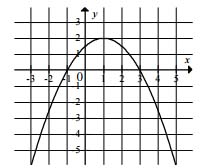
Funkcja \(f\) jest określona wzorem
A. \(f(x)=\frac{1}{2}(x+3)(x-1)\)
B. \(f(x)=\frac{1}{2}(x-3)(x+1)\)
C. \(f(x)=-\frac{1}{2}(x+3)(x-1)\)
D. \(f(x)=-\frac{1}{2}(x-3)(x+1)\)

Zadanie nr 4 — maturalne.
Pierwiastki \(x_1\), \(x_2\) równania \(2(x+2)(x-2)=0\) spełniają warunek:
A. \(\frac{1}{x_1}+\frac{1}{x_2}=-1\)
B. \(\frac{1}{x_1}+\frac{1}{x_2}=0\)
C. \(\frac{1}{x_1}+\frac{1}{x_2}=\frac{1}{4}\)
D. \(\frac{1}{x_1}+\frac{1}{x_2}=\frac{1}{2}\)

Zadanie nr 5 — maturalne.
Funkcja kwadratowa określona jest wzorem \(f(x)=-2(x+3)(x-5)\). Liczby \(x_1, x_2\) są różnymi miejscami zerowymi funkcji \(f\). Zatem
- \(x_1+x_2=-8\)
- \(x_1+x_2=-2\)
- \(x_1+x_2=2\)
- \(x_1+x_2=8\)
Powiązane materiały
© medianauka.pl, 2009-07-19, A-269
Data aktualizacji artykułu: 2023-04-21

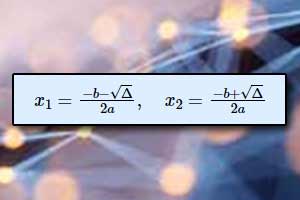 Miejsca zerowe funkcji kwadratowej
Miejsca zerowe funkcji kwadratowej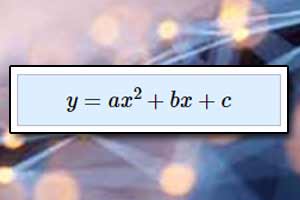 Funkcja kwadratowa
Funkcja kwadratowa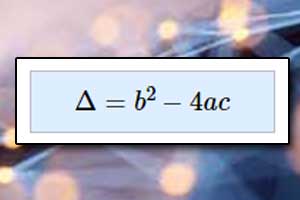 Postać kanoniczna funkcji kwadratowej
Postać kanoniczna funkcji kwadratowej Parabola
Parabola Właściwości i wykres funkcji kwadratowej
Właściwości i wykres funkcji kwadratowej