Nauka » Matematyka » Postać iloczynowa trójmianu kwadratowego

Zadanie maturalne nr 6, matura 2018

Treść zadania:

Funkcja kwadratowa określona jest wzorem \(f(x)=-2(x+3)(x-5)\). Liczby \(x_1, x_2\) są różnymi miejscami zerowymi funkcji \(f\). Zatem

Rozwiązanie zadania

Mamy do czynienia z funkcją kwadratową w postaci iloczynowej:

\( y=a(x-x_1)(x-x_2) \)

Stąd od razu możemy odczytać wartości pierwiastków:

\( x_1=-3, x_2=5\)

Zatem:

\(x_1+x_2=-3+5=2 \)

Odpowiedź C

Matura z matematyki

Zbiór zadań maturalnych z ubiegłych lat na poziomie podstawowym i rozszerzonym oraz centrum dowodzenia dla maturzystów.

Zbiór zadań z matematyki

Zbiór zadań z matematyki wraz z pełnymi rozwiązaniami. W naszej bazie zgromadziliśmy ponad tysiąc zadań.

WYKRESY ONLINE

Narysuj wykres funkcji w programie do szkicowania wykresów i odczytaj jego własności.

Zadanie nr 1.

Przedstawić funkcję

a) \(f(x)=-x^2+7x-12\)

b) \(f(x)=2x^2+44x+242\)

w postaci iloczynowej.

Zadanie nr 2.

Zapisać wzór funkcji kwadratowej, która ma dwa miejsca zerowe \(x_1=-1\) oraz \(x_2=5\), wiedząc że parabola przecina oś OY w punkcie (0,15).

Zadanie nr 3 — maturalne.

Na rysunku przedstawiono fragment wykresu funkcji kwadratowej \(f\).

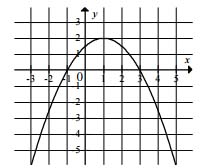
zadanie 7, matura 2014

Funkcja \(f\) jest określona wzorem

A. \(f(x)=\frac{1}{2}(x+3)(x-1)\)

B. \(f(x)=\frac{1}{2}(x-3)(x+1)\)

C. \(f(x)=-\frac{1}{2}(x+3)(x-1)\)

D. \(f(x)=-\frac{1}{2}(x-3)(x+1)\)

Zadanie nr 4 — maturalne.

Pierwiastki \(x_1\), \(x_2\) równania \(2(x+2)(x-2)=0\) spełniają warunek:

A. \(\frac{1}{x_1}+\frac{1}{x_2}=-1\)

B. \(\frac{1}{x_1}+\frac{1}{x_2}=0\)

C. \(\frac{1}{x_1}+\frac{1}{x_2}=\frac{1}{4}\)

D. \(\frac{1}{x_1}+\frac{1}{x_2}=\frac{1}{2}\)