Monotoniczność funkcji
Monotoniczność jest to pewna cecha funkcji, która mówi nam, co się dzieje z wartościami funkcji podczas zwiększania wartości liczbowych argumentów funkcji. I tak wyróżniamy z tego względu funkcje:
- rosnące
- malejące
- nierosnące
- niemalejące
Warto tu jeszcze wspomnieć o funkcji stałej, choć nie mówimy o niej jak o funkcji monotonicznej.
Funkcja stała
Funkcja stała to taka funkcja, która przyjmuje takie same wartości dla dowolnych argumentów.
Przykłady
Są to przykładowo funkcje:
- \(f(x)=5\)
- \(f(x)=0\)
- \(f(x)=-111\)
Funkcja rosnąca
Funkcja \(f(x)\) jest rosnąca w zbiorze \(A\), gdy dla dowolnych dwóch liczb \(x_1,\ x_2\) z tego zbioru prawdziwa jest implikacja:
Pojęcie funkcji rosnącej można wyobrazić sobie w następujący sposób. Jeżeli będziemy zwiększać w całym rozpatrywanym przedziale argumenty funkcji i zaobserwujemy, że rosną też wartości funkcji dla tych argumentów, to mamy do czynienia z funkcją rosnącą w tym przedziale.
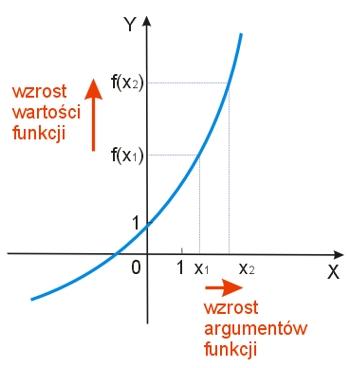
Cechą charakterystyczną wykresu funkcji rosnącej jest to, że zdaje się wznosić ku górze.
Jak zbadać, czy dana funkcja jest rosnąca?
Przykłady
Wykażemy, że funkcja \(f(x)=3x-2\) jest rosnąca w całej dziedzinie.
Zakładamy, że \(x_1<x_2\).
Obliczamy
\(f(x_1)=3x_1-2\)
\(f(x_2)=3x_2-2\)
Musimy wykazać, że
\(f(x_1)<f(x_2)\), czyli \(f(x_2)-f(x_1)>0\).
Podstawiamy do nierówności wyliczone wartości funkcji i otrzymujemy:
\(3x_2-2-(3x_1-2)>0\)
\(3x_2-2-3x_1+2>0\)
\(3x_2-3x_1>0\)
\(x_2-x_1>0\)
\(x_1<x_2\)
Jest to zgodne z założeniem. A więc funkcja ta jest rosnąca w całej swojej dziedzinie.
Funkcja malejąca
Funkcja \(f(x)\) jest malejąca w zbiorze \(A\), gdy dla dowolnych dwóch liczb \(x_1,\ x_2\) z tego zbioru prawdziwa jest implikacja:
Pojęcie funkcji malejącej można wyobrazić sobie w następujący sposób. Jeżeli będziemy zwiększać w całym rozpatrywanym przedziale argumenty funkcji i zaobserwujemy, że maleją wartości funkcji dla tych argumentów, to mamy do czynienia z funkcją malejącą w tym przedziale.
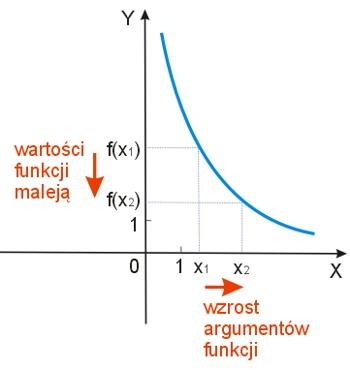
Cechą charakterystyczną wykresu funkcji malejącej jest to, że zdaje się opadać w dół.
Jak zbadać, czy dana funkcja jest malejąca?
Przykłady
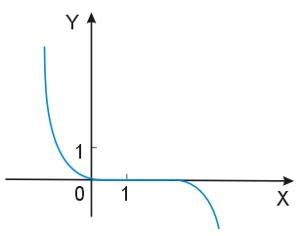
Wykażemy, że funkcja \(f(x)=\frac{1}{x}\) jest malejąca w zbiorze liczb rzeczywistych dodatnich, czyli w zbiorze \(\mathbb{R}_+\).
Zakładamy, że \(x_1<x_2\), czyli \(x_2-x_1>0\).
Obliczamy:
\(f(x_1)=\frac{1}{x_1}\)
\(f(x_2)=\frac{1}{x_2}\)
Musimy wykazać, że
\(f(x_1)>f(x_2)\), czyli \(f(x_1)-f(x_2)>0\).
Podstawiamy do nierówności wyliczone wartości funkcji i otrzymujemy:
\(\frac{1}{x_1}-\frac{1}{x_2}>0\)
\(\frac{x_2-x_1}{x_1x_2}>0\)
Przeanalizujmy powyższe wyrażenie. Licznik zgodnie z założeniem jest większy od zera. Jeżeli chodzi o mianownik, to zauważamy, że rozpatrujemy liczby z dziedziny funkcji, a więc jedynie liczby dodatnie, których iloczyn jest również dodatni. Ułamek, którego licznik i mianownik jest większy od zera jest oczywiście większy od zera. Oznacza to, że nierówność, którą rozpatrujemy jest prawdziwa dla każdego \(x_1,\ x_2\), co należało dowieść. Funkcja ta jest więc malejąca w rozpatrywanym zbiorze.
Przedziały monotoniczności
Czy funkcja może być jednocześnie malejąca i rosnąca w różnych przedziałach liczbowych? Oczywiście, że tak. Poniżej przykład takiej funkcji wraz z określonymi przedziałami, w których funkcja rośnie i maleje oraz jest stała.
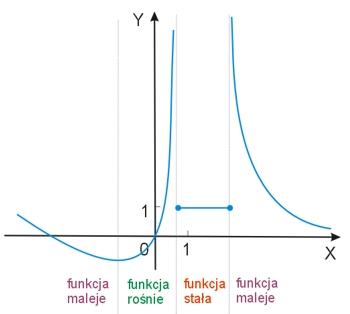
W takim przypadku badając monotoniczność, określamy przedziały, w których funkcja jest rosnąca, malejąca lub stała.
Funkcja niemalejąca
Funkcja \(f(x)\) jest niemalejąca w zbiorze \(A\), gdy dla dowolnych dwóch liczb \(x_1,\ x_2\) z tego zbioru prawdziwa jest implikacja:
Zatem definicja funkcji niemalejącej przypomina definicję funkcji rosnącej, z tym że w przypadku funkcji niemalejącej mamy nieostrą nierówność. Dopuszczamy więc przedziały, w których funkcja jest stała.
Oto ilustracja funkcji niemalejącej.
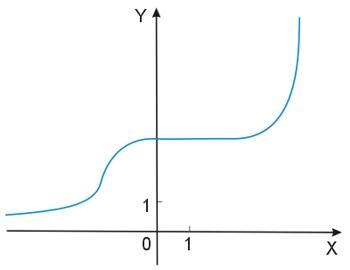
Funkcja nierosnąca
Funkcja \(f(x)\) jest nierosnąca w zbiorze \(A\), gdy dla dowolnych dwóch liczb \(x_1, x_2\) z tego zbioru prawdziwa jest implikacja:
Zatem definicja funkcji nierosnącej przypomina definicję funkcji malejącej, z tym że w przypadku funkcji nierosnącej mamy nieostrą nierówność. Dopuszczamy więc przedziały, w których funkcja jest stała.
Oto ilustracja funkcji nierosnącej.
Pytania
Jakie są przykłady funkcji rosnącej, malejącej i stałej?
Na przykład funkcja \(y=x\) jest funkcją rosnącą, funkcja \(y=-2x\) to funkcja malejąca. Funkcja stała to na przykład funkcja \(y=-1\).
Czy funkcja liniowa ma przedziały monotoniczności?
Monotoniczność funkcji liniowej \(y=ax+b\):
- funkcja liniowa jest stała, gdy współczynnik kierunkowy prostej \(a\) jest równy zeru,
- funkcja liniowa jest rosnąca, gdy współczynnik \(a\) jest większy od zera,
- funkcja liniowa jest malejąca, gdy współczynnik kierunkowy prostej jest ujemny.
Jak przebiega badanie monotoniczności funkcji?
Jeżeli dana jest funkcja \(f(x)\), zakładamy, że \(x_1<x_2\) i wykazujemy, że:
- \( f(x_1)>f(x_2)\) w przypadku funkcji malejącej,
- \(f(x_1)<f(x_2)\) w przypadku funkcji rosnącej,
- \(f(x_1)=f(x_2)\) w przypadku funkcji stałej.
Tak postępujemy dla prostych funkcji.
Znacznie wygodniejsze i łatwiejsze jest badanie monotoniczności funkcji przy pomocy pochodnej funkcji. Polecamy artykuł Pochodna a monotoniczność funkcji.
Jak zbadać monotoniczność funkcji kwadratowej?
Monotoniczność funkcji kwadratowej omawiamy w artykule Wykres funkcji kwadratowej.
Zadania z rozwiązaniami

Zadanie nr 1.
Wykazać na podstawie definicji, że funkcja \(f(x)=\frac{x}{2}-3\) jest rosnąca w całej swojej dziedzinie.

Zadanie nr 2.
Wykazać na podstawie definicji, że funkcja \(f(x)=5-x\) jest malejąca w całej swojej dziedzinie.

Zadanie nr 3.
Wykazać na podstawie definicji, że funkcja \(f(x)=x^2\) jest rosnąca dla \(x>0\).
Powiązane materiały
 Monotoniczność funkcji
Monotoniczność funkcji© medianauka.pl, 2009-05-06, A-202
Data aktualizacji artykułu: 2023-04-02

 Pochodna a monotoniczność funkcji
Pochodna a monotoniczność funkcji Miejsce zerowe funkcji
Miejsce zerowe funkcji Funkcja okresowa
Funkcja okresowa Parzystość funkcji
Parzystość funkcji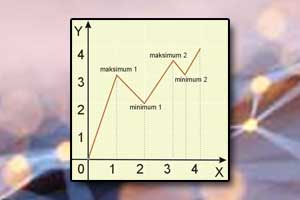 Ekstremum funkcji
Ekstremum funkcji Funkcja różnowartościowa
Funkcja różnowartościowa Własności funkcji
Własności funkcji Monotoniczność funkcji — quiz
Monotoniczność funkcji — quiz