Parzystość funkcji

Zajmiemy się w tym artykule własnością parzystości i nieparzystości dowolnej funkcji.

Funkcja parzysta

Funkcję \(f\) nazywamy parzystą, gdy dla każdej liczby \(x\) należącej do dziedziny tej funkcji liczba do niej przeciwna również należy do dziedziny tej funkcji i \(f(-x)=f(x)\).

Przykłady

Oto przykłady funkcji parzystych:

\(f(x)=\cos{x}\), bo \( \cos x=\cos{(-x)}\)
\(f(x)=x^2\), bo \( x^2=(-x)^2\)
\(f(x)=x^4\), bo \( x^4=(-x)^4\)
\(f(x)=\frac{1}{x^2}\), bo \(\frac{1}{x^2}=\frac{1}{(-x)^2}\)

Dla funkcji parzystej wykres przyjmuje charakterystyczną postać, a mianowicie jest on symetryczny względem osi OY (jest odbiciem lustrzanym względem tej osi).

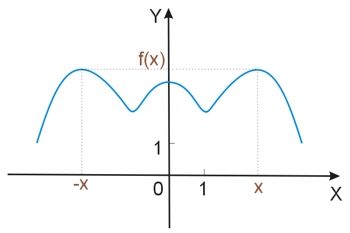
Funkcja nieparzysta

Funkcję \(f\) nazywamy nieparzystą, gdy dla każdej liczby \(x\) należącej do dziedziny tej funkcji liczba do niej przeciwna również należy do dziedziny tej funkcji i \(f(-x)=-f(x)\).

Przykłady

Przykłady funkcji nieparzystych:

\(f(x)=\sin{x}\), bo \( \sin (-x)=-\sin{x}\)
\(f(x)=x^3, bo (-x)^3=-x^3\)
\(f(x)=\frac{1}{x^5}\), bo \( \frac{1}{(-x)^5}=-\frac{1}{x^5}\)

Dla funkcji nieparzystej wykres przyjmuje charakterystyczną postać, a mianowicie jest on symetryczny względem początku układu współrzędnych.

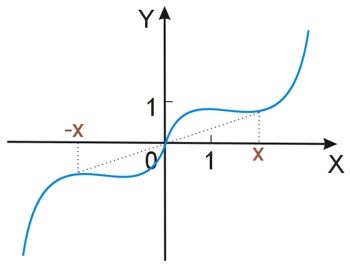
funkcja nieparzysta

Przykłady

Rozpatrzmy funkcję \(f(x)=2x+1\).

Sprawdźmy, czy jest to funkcja parzysta, czy nieparzysta. W tym celu sprawdzamy, jak się zachowuje funkcja dla argumentu równego \(-x\).

Sprawdzamy, czy dana funkcja jest parzysta: \(f(-x)=2(-x)+1=-2x+1 \neq f(x)\), a więc nie jest to funkcja parzysta.
Sprawdzamy, czy nasza funkcja jest nieparzysta. Znamy już wartość \(f(-x)\), wystarczy obliczyć \(-f(x)=-(2x+1)=-2x-1 \neq f(-x)\). Zatem nasza funkcja nie jest też nieparzysta.

Jak wynika z prostego przykładu, który został zaprezentowany wyżej, istnieją funkcje, które nie są ani parzyste, ani nieparzyste.