Funkcja okresowa

Co to jest funkcja okresowa?

Liczba T to okres funkcji.

Poniższy rysunek ilustruje przykładową funkcję okresową. Okresowość funkcji najlepiej widać na jej wykresie.

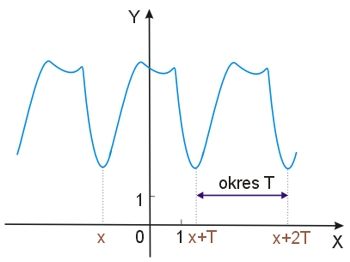
Okres podstawowy

Dla argumentu \(x, x+T, x+2T\) i tak dalej, wartości funkcji zilustrowanej na powyższym rysunku są takie same, \(T\) jest zatem okresem tej funkcji. Zauważmy jednak, że każda wielokrotność \(T\) jest również okresem funkcji. Z tego powodu za okres podstawowy funkcji przyjmuje się najmniejszy dodatni z okresów funkcji.

Przykłady funkcji okresowych

Najczęściej wykorzystywane funkcje okresowe, to funkcje trygonometryczne:

• \(y=sinx\),
• \(y=cosx\),
• \(y=tgx\),
• \( y=ctgx\).

Dla przykładu okresem funkcji \(y=\sin{x}\) jest liczba \(\pi\).

Co ciekawe, funkcja stała, na przykład y=2, również jest funkcją okresową. Nie posiada ona jednak okresu podstawowego.

Innym przykładem funkcji okresowej jest funkcja \(y=x-|x|\).

Zadania z rozwiązaniami

Zadanie nr 1.

Znaleźć okres podstawowy funkcji

a) \(y=\sin{2x}\)

b) \(y= \sin{\pi x}\)

Pokaż rozwiązanie zadania.

Zadanie nr 2.

Znaleźć okres podstawowy funkcji \(y=\cos{4x}\).

Pokaż rozwiązanie zadania.

Zadanie nr 3.

Znaleźć okres podstawowy funkcji \(y = tg4x\).

Pokaż rozwiązanie zadania.

Zadanie nr 4.

Znaleźć okres podstawowy funkcji: \(y=\frac{1}{2}tg{(\frac{\pi}{2}x)}\).

Pokaż rozwiązanie zadania.

Zadanie nr 5.

Znaleźć okres podstawowy funkcji:

a) \(y=3ctg{\frac{x}{\pi}}\)

b) \(y=2\cos{(x+\frac{\pi}{7})}\)

Pokaż rozwiązanie zadania.

Zadanie nr 6.

Znaleźć okres podstawowy funkcji:

Pokaż rozwiązanie zadania.

Zadanie nr 7.

Znaleźć okres podstawowy funkcji: \(y=\cos^4{x}-\sin^4{x}\).

Pokaż rozwiązanie zadania.

Powiązane materiały

Miejsce zerowe funkcji

Monotoniczność funkcji

Parzystość funkcji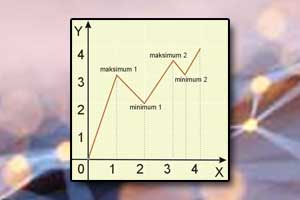

Ekstremum funkcji

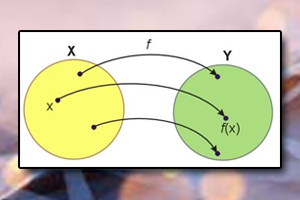Funkcja różnowartościowa

Własności funkcji

Własności funkcji

© medianauka.pl, 2009-05-07, A-203
Data aktualizacji artykułu: 2023-04-02