Równanie wielomianowe
Równanie w postaci \(W(x)=0\), gdzie \(W(x)\) jest wielomianem niezerowym, nazywamy równaniem algebraicznym lub równaniem n-tego stopnia, lub równaniem wielomianowym.
Przykłady
Przykłady równań algebraicznych:
- \(x^3+x-1=0\) — jest to równanie 3. stopnia.
- \(x^5+5x^3-x-33=0\) — jest to równanie 5. stopnia.
- \(5x^2+7=0\) — jest to równanie 2. stopnia (kwadratowe).
- \(x-1=0\) — jest to równanie 1. stopnia.
Twierdzenie
Równanie algebraiczne \(n\)-tego stopnia ma co najwyżej \(n\) różnych pierwiastków (rozwiązań).
Twierdzenie
Jeżeli wielomian \(n\)-tego stopnia ma \(n\) różnych pierwiastków \(x_1,x_2,x_3,...,x_n\), to
\(W(x)=a_n(x-x_1)(x-x_2)(x-x_3)\cdot{...}\cdot{(x-x_n)}\),
gdzie \(a_n\) jest czynnikiem przy \(x^n\).
Twierdzenie
Każde równanie algebraiczne nieparzystego stopnia ma co najmniej jeden pierwiastek.
Jak rozwiązać równanie algebraiczne?
Rozwiązanie równania algebraicznego często sprowadza się do rozkładu wielomianu na czynniki, a każdy z tych czynników możemy przyrównać do zera i otrzymać w ten sposób rozwiązania.
Można też zastosować następujący schemat rozwiązania równania algebraicznego:
- Szukamy pierwiastka \(a\) równania wśród podzielników wyrazu wolnego.
- Dzielimy wielomian przez \((x-a)\).
- Otrzymany iloraz przyrównujemy do zera.
- W zależności od stopnia otrzymanego równania powtarzamy procedurę lub stosujemy inną znaną metodę.
Oto kilka przykładów rozwiązań równań wielomianowych.
Przykład 1
Rozwiązać równanie \(x^3-2x^2+x-2=0\).
Szukamy pierwiastków pośród liczb 1, -1, 2 i -2 (dzielniki wyrazu wolnego).
\(W(1)=1-2+1-2=-2\neq{0}\)
\(W(-1)=-1-2-1-2=-6\neq{0}\)
\(W(2)=8-8+2-2=0\)
\(W(-2)=-8-8-2-2=-20\neq{0}\)
Znaleźliśmy jeden pierwiastek równy liczbie 2. Zatem wielomian \(W(x)=x^3-2x^2+x-2\) dzieli się przez \((x-2)\).
Wykonajmy to dzielenie.
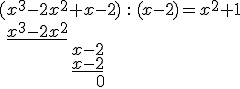
Możemy zapisać równanie w następującej postaci:
\(W(x)=x^3-2x^2+x-2=(x-2)(x^2+1)=0\)
Ponieważ \(x^2+1<0\) jedynym pierwiastkiem równania jest liczba 2.
Odpowiedź: \(x=2\).
Przykład 2
Rozwiązać równanie \(-2x^3+3x^2+3x-2=0\).
Szukamy pierwiastków pośród liczb 1, -1, 2 i -2 (dzielniki wyrazu wolnego).
\(W(1)=-2+3+3-2=2\neq{0}\)
\(W(-1)=2+3-3-2=0\)
Znaleźliśmy jeden pierwiastek równy liczbie -1. Zatem nasz wielomian dzieli się przez \((x+1)\).
Wykonajmy to dzielenie.
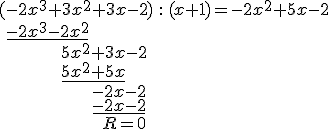
Możemy zapisać równanie w następującej postaci:
\(W(x)=-2x^3+3x^2+3x-2=(x+1)(-2x^2+5x-2)=0\).
Drugi czynnik to nic innego jak trójmian kwadratowy, rozkładamy go więc na czynniki.
\(a=-2, b=5, c=-2\)
\({\Delta=b^2-4ac=25-16=9}\)
\(x_1=\frac{-b-sqrt{\Delta}}{2a}=\frac{-5-3}{-4}=2\)
\(x_2=\frac{-b+sqrt{\Delta}}{2a}=\frac{-5+3}{-4}=\frac{1}{2}\)
Możemy zapisać równanie w następującej postaci:
\(W(x)=-2x^3+3x^2+3x-2=(x+1)(-2x^2+5x-2)=(x+1)(x-2)(x-\frac{1}{2})=0\)
Odpowiedź: \(x_1=-1, x_2=\frac{1}{2}, x_3=2\).
Twierdzenie
Jeżeli niezerowa liczba wymierna \(\frac{p}{q}\) (ułamek nieskracalny) jest pierwiastkiem równania \(W(x)=a_{n}x^{n}+a_{n-1}x^{n-1}+...+a_1x+a_0=0\), gdzie \(a_n,\ a_{n-1},\ ...,a1 \ , a0\) są współczynnikami całkowitymi i \(a_0\cdot{a_n}\neq{0}\), to \(p\) jest podzielnikiem wyrazu wolnego \(a_0\), a \(q\) jest podzielnikiem współczynnika \(a_n\).
Przykład
W przypadku, gdy współczynnik \(a_n\) jest różny od jedności, możemy typować także ułamki pośród pierwiastków równania algebraicznego. Oto taki przykład.
Znajdźmy powyższą metodą pierwiastki równania \(6x^2-x-1=0\).
Podzielniki p wyrazu wolnego: 1, -1
Podzielniki q współczynnika przy najwyższej potędze niewiadomej: 1,-1,2,-2,3,-3
Możliwe pierwiastki \(\frac{p}{q}\): \(1,-1,\frac{1}{2},-\frac{1}{2},\frac{1}{3},-\frac{1}{3}\).
Sprawdźmy kolejno wartości wielomianów dla tych liczb.
\(W(1)=6-1-1=4\neq{0}\)
\(W(-1)=6+1-1=6\neq{0}\)
\(W(\frac{1}{2})=6\cdot \frac{1}{4}-\frac{1}{2}-1=\frac{3}{2}-\frac{1}{2}-1=0\)
\(W(-\frac{1}{2})=6\cdot \frac{1}{4}+\frac{1}{2}-1=\frac{3}{2}+\frac{1}{2}-1=1\neq{0}\)
\(W(\frac{1}{3})=6\cdot \frac{1}{9}-\frac{1}{3}-1=\frac{2}{3}-\frac{1}{3}-1=-\frac{2}{3}\neq{0}\)
\(W(-\frac{1}{3})=6\cdot \frac{1}{9}+\frac{1}{3}-1=\frac{2}{3}+\frac{1}{3}-1=0\)
A więc znaleźliśmy dwa pierwiastki (rozwiązania równania). Zapiszmy jeszcze postać iloczynową wielomianu.
\(6(x-\frac{1}{2})(x+\frac{1}{3})=0\)
Zadania z rozwiązaniami
Zadanie nr 1 — maturalne.
Suma wszystkich pierwiastków równania \((x+3)(x+7)(x-11)=0\) jest równa:
A. \(-1\)
B. \(21\)
C. \(1\)
D. \(-21\)
Zadanie nr 3 — maturalne.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. Jednym z rozwiązań równania \(\sqrt{3}(x^2-2)(x+3)=0\) jest liczba
A. 3
B. 2
C. \(\sqrt{3}\)
D. \(\sqrt{2}\)
Zadanie nr 4 — maturalne.
Iloczyn wszystkich rozwiązań równania \(2x(x^2-9)(x+1)=0\) jest równy
A. -3
B. 3
C. 0
D. 9
Zadanie nr 6 — maturalne.
Suma wszystkich rozwiązań równania \(x(x−3)(x+2)=0\) jest równa
A. 0
B. 1
C. 2
D. 3
Zadanie nr 10 — maturalne.
Wspólnym pierwiastkiem równań \((x^2-1)(x-10)(x-5)=0\) i \(\frac{2x-10}{x-1}=0\) jest liczba:
A. -1
B. 1
C. 5
D. 10
Zadanie nr 14.
Dla jakich wartości parametrów \(a\) i \(b\) równanie \(x^4-6x^3+10x^2-bx+a=0\) ma podwójny pierwiastek, równy 3?
Zadanie nr 17.
Rozwiązać równanie wielomianowe \(x^6-6x^5+x^4+16x^3+15x^2+22x+15=0\).
Zadanie nr 18.
Rozwiązać równanie wykładnicze \((\frac{1}{2})^{x-1}-2^{2x}-1=0\).
Zadanie nr 19.
Wyznaczyć dziedzinę funkcji \(f(x)=\frac{x^4-x^3+x^2+6x-1}{6x^3-5x^2-2x+1}\)
Zadanie nr 20.
Wyznaczyć dziedzinę funkcji \(f(x)=\frac{3x^2-2x+1}{2x^3-3x^2-2x}\).
Inne zagadnienia z tej lekcji
Równanie algebraiczne
Nierówność wielomianowa
Układ równań algebraicznych
Równanie wymierne© medianauka.pl, 2009-08-18, A-286
Data aktualizacji artykułu: 2023-05-09