Nauka » Matematyka » Proporcjonalność prosta

Zadanie - proporcjonalność prosta

Sekretarka potrafi napisać średnio 50 słów w ciągu jednej minuty na komputerze. Jak długo potrwa ręczne przepisanie książki o objętości 240 stron, jeżeli wiadomo, że średnio jedna strona maszynopisu zawiera 250 słów, a sekretarka jest jednego dnia w stanie pisać bez przerwy przez 5 godzin?

Rozwiązanie zadania uproszczone

1 strona	-	250 wyrazów
240 stron	-	x wyrazów

$x=240\cdot 250 \\ x=60000$
Średnio książka o objętości 240 stron zawiera 60 000 wyrazów

50 słów	-	1 min
60 000 słów	-	x min

$50x=1\cdot 60000/:50 \\ x=1200$
Przepisanie książki zajmie sekretarce 1200 minut = 20 h

1 dzień	-	5 h
x dni	-	20 h

$5x=20/:5 \\ x=4$
Przepisanie książki potrwa 4 dni.

Rozwiązanie zadania ze szczegółowymi wyjaśnieniami

Mamy do czynienia ze złożonym zagadnieniem, rozbijemy więc zadanie na kilka części. Policzymy najpierw ile wyrazów średnio liczy książka o objętości 240 stron. Układamy proporcję:

1 strona	-	250 wyrazów
240 stron	-	x wyrazów

Zakładamy tutaj, że liczba wyrazów jest proporcjonalna do liczby stron. Iloraz tych wielkości zatem nie zmienia się (wiemy to na podstawie określenia proporcjonalności prostej), możemy więc zapisać:

$\frac{1}{240}=\frac{250}{x}$

a najlepiej od razu pomnożyć te liczby "na krzyż":

$x=240\cdot 250 \\ x=60000$

Wiemy więc, że średnio książka o objętości 240 stron zawiera 60 000 wyrazów

Policzymy teraz ile czasu zajmie sekretarce przepisanie 60 000 wyrazów, wiemy bowiem jak długo przepisuje 50 słów. Ponownie układamy proporcję:

50 słów	-	1 min
60 000 słów	-	x min

Zakładamy tutaj, że liczba napisanych wyrazów jest proporcjonalna do czasu ich pisania. Iloraz tych wielkości zatem nie zmienia się (wiemy to na podstawie określenia proporcjonalności prostej), możemy więc zapisać:

$\frac{50}{60000}=\frac{1}{x}$

a najlepiej od razu pomnożyć te liczby "na krzyż":

$50x=1\cdot 60000/:50 \\ x=1200$

Wiemy więc, że przepisanie książki zajmie sekretarce 1200 minut. Ponieważ 1 h = 60 minut:

$1200 min=\frac{1200}{60} h=20 h$

Jeżeli nie wiesz skąd wziął się ten wynik, to można było tutaj również zastosować proporcję:

1 h	-	60 min
x h	-	1200 min

$60x=1200/:60 \\ x=20$

Wiemy ponadto, że sekretarka potrafi w jednym dniu pracować bez przerwy tylko 5 godzin. Możemy więc policzyć od razu ile dni zajmie praca nad przepisaniem książki albo kolejny raz zastosować proporcję:

1 dzień	-	5 h
x dni	-	20 h

$5x=20/:5 \\ x=4$

Odpowiedź

Przepisanie książki potrwa 4 dni.

Zadania podobne

Zadanie - proporcjonalność prosta
Średnio tygodniowo autor pewnego bloga zarabia na wyświetlaniu reklam na swojej stronie 20 zł. Jakiego zysku może się spodziewać po roku prowadzenia strony?

Pokaż rozwiązanie zadania

Zadanie - proporcjonalność prosta
Babcia w ciągu godziny potrafi wydziergać 20 cm szalika. Ile czasu potrwa wydzierganie całego szalika o długości półtora metra?

Pokaż rozwiązanie zadania

Zadanie - proporcjonalność prosta
Śnieg padał jednostajnie przez 6,5 h. Spadło 19,5 cm śniegu. Ile śniegu spadło w ciągu jednej godziny?

Pokaż rozwiązanie zadania

Zadanie - proporcjonalność prosta
Jeden pracownik składa 500 długopisów w ciągu ośmiu godzin pracy. Ilu pracowników trzeba zatrudnić, aby wykonać zlecenie złożenia 10 000 długopisów w ciągu pięciu dni?

Pokaż rozwiązanie zadania

Zadanie - proporcjonalność prosta - wykres
Wykres ilustruje zależność zaoszczędzonych środków na lokacie od czasu oszczędzania.

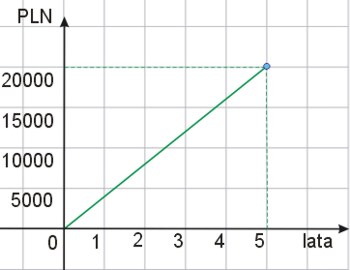
Ile pieniędzy zaoszczędzono po 3 latach oszczędzania?

Pokaż rozwiązanie zadania

Zadanie - proporcjonalność prosta
Podczas ostatniego tankowania kierowca wyzerował licznik, przejechał 654 kilometry i zatankował do pełna. Do baku zmieściło się 34,5 l benzyny. Ile litrów na sto kilometrów spala silnik tego samochodu?

Pokaż rozwiązanie zadania

Niektóre treści nie są dostosowane do Twojego profilu. Jeżeli jesteś pełnoletni możesz wyrazić zgodę na przetwarzanie swoich danych osobowych. W ten sposób będziesz miał także wpływ na rozwój naszego serwisu.