Pole figury

Pole figury płaskiej jest to funkcja, która każdej figurze geometrycznej płaskiej przyporządkowuje liczbę nieujemną w taki sposób, że spełnione są warunki:

pola figur przystających są równe,
jeżeli figury nie mają punktów wspólnych, to pole figury stanowiących ich sumę jest sumą pól figur składowych.

Nie dla każdej figury pole musi istnieć.

Pole figury wyrażamy w jednostkach pola. Za jednostkę pola będziemy przyjmować pole kwadratu o boku długości równej przyjętej jednostce długości. Jeżeli \(\overline{u}\) jest jednostkową długością, to \(\overline{u}^2\) stanowi jednostkę pola. Czyli jeżeli za jednostkę długości przyjmiemy liczbę 1 cm, to pole kwadratu o boku długości 1 cm będzie jednostką pola figury i oznaczymy ją jako 1 cm².

Powyższe określenie dotyczy ogólnego pojęcia pola figury. Przejdziemy teraz do miary polowej figury płaskiej (pola figury płaskiej)

Dana jest ograniczona figura płaska \(f\). Nakładamy na nią sieć kwadratów o odstępie \(\overline{u}\) i wyznaczamy:

liczbę \(w_0\) kwadratów tej sieci zawartych w tej figurze,
liczbę \(z_0\) kwadratów pokrywających tę figurę (mających co najmniej jeden punkt wewnętrzny lub brzegowy tej figury).

Liczby te nazywamy przybliżeniem dolnym i przybliżeniem górnym pola figury.

Ilustruje to poniższy rysunek:

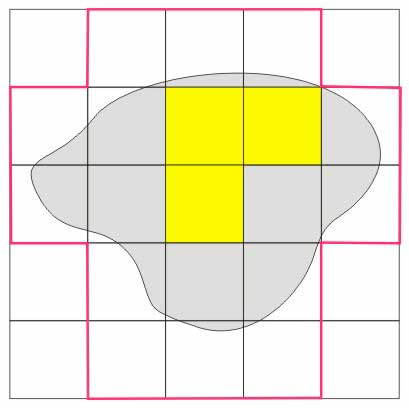
Pole figury 1

Mamy tutaj więc \(w_0=3\) (żółte pola) i \(z_0=19\) (pola otoczone czerwoną linią). Zatem zawsze \(w_0<z_0\). Dolnym przybliżeniem pola jest liczba 3, natomiast górnym przybliżeniem pola jest liczba 19. Można powiedzieć, że pole naszej figury jest liczbą z przedziału od 3 do 19. To dość kiepskie przybliżenie. Teraz na naszą sieć wyjściową nałożymy sieć o mniejszym odstępie (każdy kwadrat sieci podzielimy na cztery części).

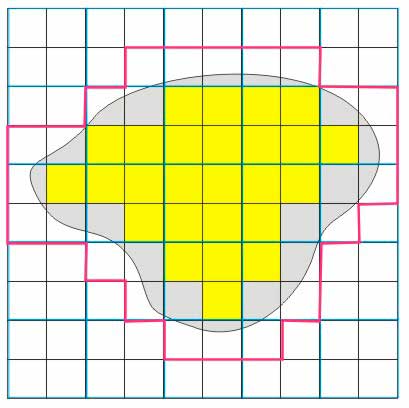
Pole figury 2

Teraz wyznaczamy liczbę \(w_1\), która wyraża w tych samych jednostkach \(\overline{u}^2\) łączne pole kwadratów sieci zawartych w danej figurze (żółte pola) oraz liczbę \(z_1\), która wyraża w tych samych jednostkach \(\overline{u}^2\) łączne pole kwadratów sieci pokrywających figurę (kwadraty zaznaczone czerwoną obwódką). Czyli w naszym przypadku mamy 26 żółtych kwadratów, co daje liczbę \(w_1=6,5\) (26 małych kwadratów składa się na pole 6,5 większych kwadratów). Liczba \(z_1=14\) (56 małych kwadratów daje 14 pola dużego — jednostkowego kwadratu). Mamy więc kolejne przybliżenie pola. Teraz możemy powiedzieć, że pole naszej figury jest liczbą z przedziału od 6,5 do 14. Możemy też zapisać, że \(w_0\leq w_1 < z_1\leq z_0\).

W ten sposób możemy nakładać kolejne siatki na figurę, otrzymując ciągi liczb \(w_0\leq w_1 \leq w_2\leq ... \leq w_n< z_n\leq ... \leq z_1\leq z_0\). Ciągi te są monotoniczne i ograniczone, więc są zbieżne (posiadają granice):

\(\lim{w_n}=w(f)\)

\(\lim{z_n}=z(f)\)

Liczby te nazywamy następująco:
\(w(f)\) — wewnętrzna miara pola figury \(f\),
\(z(f)\) — zewnętrzna miara pola figury \(f\),
przy czym \(w(f)\leq z(f)\).

Polem figury f (miarą polową figury \(f\)) nazywamy liczbę \(m(f)=\lim{w_n}=\lim{z_n}\), czyli mamy przypadek \(w(f)=z(f)\).

Własności pola

Oto kilka istotnych własności pola:

pole figury nie zależy od sieci wyjściowej,
każda figura zawarta w odcinku ma pole równe 0,
każda łamana ma pole 0,
każdy łuk okręgu ma pole 0,
jeśli brzeg figury ma pole 0, to figura \(f\) ma pole \(m(f)\),
każda figura ograniczona , której brzeg składa się ze skończonej liczby odcinków lub łuków ma pole,
pole wielokąta można obliczyć, dzieląc go na trójkąty i dodając do siebie pola tych trójkątów.

Pola figur takich jak koło, trójkąt, kwadrat, prostokąt, trapez, romb, równoległobok zostały przedstawione w lekcjach poświęconych tym figurom.

Pola figur geometrycznych

Poniższa tabela zawiera podstawowe wzory na pola figur płaskich.

Figura geometryczna	Wzór na pole powierzchni
kwadrat	\(P=a^2\)
prostokąt	\(P=ab\)
trójkąt	\(P=\frac{1}{2}ah\)
romb	\(P=ah\)
równoległobok	\(P=ah_1=bh_2\)
trapez	\(P=\frac{1}{2}(a+b)\cdot h\)
deltoid	\(P=\frac{1}{2}d_1d_2\)
koło	\(P=\pi r^2\)
elipsa	\(P=\pi ab\)

Są to tylko najczęściej wykorzystywane w kursie matematyki wzory. Dla wielu figur obowiązują także inne wzory, omawiane odrębnie w artykułach poświęconych danej figurze geometrycznej. Kilka przydatnych wzorów na pole powierzchni wielokąta foremnego znajdziesz w artykule o wielokątach foremnych.

Pytania

Jak obliczać pola figur?

Pola figur podstawowych obliczamy, korzystając ze wzorów powszechnie znanych (patrz powyższa tablica). Dla figur bardziej złożonych warto czasem podzielić je na trójkąty lub czworokąty, których pola możemy obliczyć i zsumować je dla uzyskania wyniku. Można także czasem użyć rachunku całkowego, gdy tylko potrafimy opisać figurę geometryczną za pomocą funkcji.