Pole koła
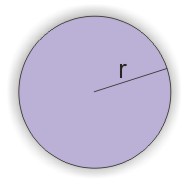
Pole koła o promieniu \(r\) jest równe:
To wzór na pole koła. Zastosujmy go w przykładach.
Przykład 1
Obliczymy pole koła o średnicy \(8\ cm\).
Koło o średnicy \(8\ cm\) ma promień o długości \(r=4\ cm\) (połowa średnicy). Pole koła jest więc równe:
\(P=\pi r^2=\pi \cdot (4 cm)^2=16\pi \ cm^2\)
Przykład 2
Oblicz ile w przybliżeniu wynosi pole koła o średnicy 2.
Jeżeli średnica ma długość 2, to promień koła ma długość 1. Stosujemy wzór na pole koła \(P=\pi r^2=\pi \cdot 1^2=\pi\approx 3,14\).
Kalkulator — pole koła

Kalkulator
Podaj długość promienia koła, a nasz kalkulator obliczy pole powierzchni koła.
Promień koła:
Wzór na pole koła ze średnicą
Jeżeli mamy podaną średnicę koła \(d\), pole koła obliczymy z następującego wzoru:
Długość okręgu
Długość okręgu to inaczej obwód koła. Podajemy wzór na obwód okręgu (długość okręgu). Długość okręgu o promieniu \(r\) jest równa:
Przykład
Obliczymy długość okręgu o średnicy 1 m.
Okrąg o średnicy 1 m ma promień o długości \(r=0,5\ m\) (połowa średnicy). Długość okręgu jest więc równa:
\(P=2\pi r=2\pi \cdot \frac{1}{2} \ m=\pi \ m\)
Pytania
Jak obliczyć pole koła?
Jeżeli znamy długość promienia, podnosimy jego wartość do kwadratu i mnożymy przez liczbę \(\pi \approx 3,14.\)
Jaka jest powierzchnia okręgu?
Okrąg ma zerowe pole powierzchni.
Zadania z rozwiązaniami

Zadanie nr 4.
Ile potrzeba sznurka, aby ułożyć z niego okrąg o średnicy 2 m?

Zadanie nr 5.
Pole koła jest równe \(\pi\). Jaki promień ma koło o polu dwa razy mniejszym? Oblicz stosunek promieni tych okręgów.

Zadanie nr 6.
Z kwadratowej blachy o boku długości 1 m wycięto koła o promieniu \(r=10\ cm\) tak, że środki tych kół leżą na prostych równoległych i prostopadłych. Jaka jest powierzchnia ścinków? Jaki procent powierzchni blachy stanowią ścinki?

Zadanie nr 7.
W koło o promieniu \(r\) wpisano kwadrat. Oblicz pole figury, która stanowi różnicę tego koła i kwadratu?

Zadanie nr 8.
Na trójkącie równobocznym o boku \(a=1\) opisano okrąg. Oblicz obwód tego okręgu i pole koła wyznaczonego przez ten okrąg.

Zadanie nr 9.
W trójkąt równoboczny o boku długości \(a=1\) wpisano koło. Oblicz jego pole i obwód.

Zadanie nr 10.
Na trójkącie prostokątnym o przyprostokątnych długości 3 i 4 opisano koło. Oblicz pole i obwód tego koła.

Zadanie nr 11.
Oblicz długość okręgu danego równaniem \((x-1)^2+(y-1)^2=2\).

Zadanie nr 12 — maturalne.
Pole figury \(F_1\) złożonej z dwóch stycznych zewnętrznie kół o promieniach 1 i 3 jest równe polu figury \(F_2\) złożonej z dwóch stycznych zewnętrznie kół o promieniach długości \(r\) (zobacz rysunek).
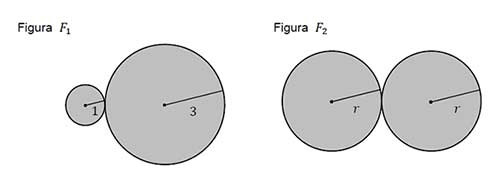
Długość \(r\) promienia jest równa
A. \(\sqrt{3}\)
B. \(2\)
C. \(\sqrt{5}\)
D. \(3\)
Wybrane karty pracy
Powiązane materiały
 Pole koła i obwód koła
Pole koła i obwód koła© medianauka.pl, 2010-12-10, A-1046
Data aktualizacji artykułu: 2023-06-13

 Okrąg i koło
Okrąg i koło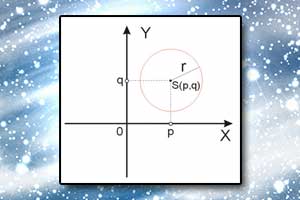 Równanie okręgu
Równanie okręgu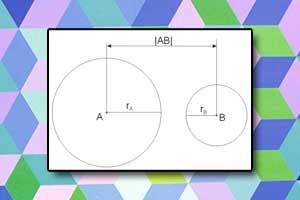 Wzajemne położenie okręgów
Wzajemne położenie okręgów Liczba pi
Liczba pi Okrąg i koło — quiz
Okrąg i koło — quiz