Wzajemne położenie dwóch okręgów

Rozpatrujemy kilka przypadków wzajemnego położenia okręgów względem siebie.

Okręgi wzajemnie zewnętrzne

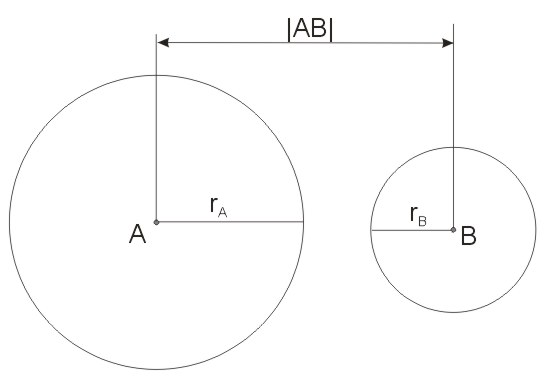
Okręgi wzajemnie zewnętrzne zostały zilustrowane na poniższym rysunku. Każdy z dwóch przedstawioną okręgów leży na zewnątrz drugiego. Jeżeli dane są promienie i środki dwóch okręgów, to dla okręgów wzajemnie zewnętrznych prawdziwa jest nierówność \(r_a+r_b<|AB|\).

okręgi wzajemnie zewnętrzne

Okręgi zewnętrznie styczne

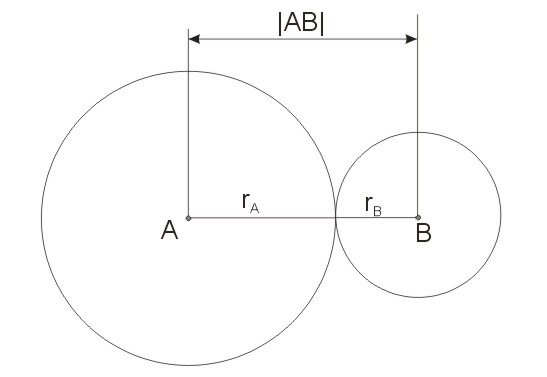
Okręgi zewnętrznie styczne zostały zilustrowane na poniższym rysunku. Oba okręgu mają tylko jeden punkt wspólny, a wszystkie pozostałe punkty jednego okręgu leżą na zewnątrz drugiego i odwrotnie. Jeżeli dane są promienie i środki dwóch okręgów, to dla okręgów zewnętrznie stycznych prawdziwa jest równość \(r_a+r_b=|AB|\).

Okręgi zewnętrznie styczne

Okręgi przecinające się

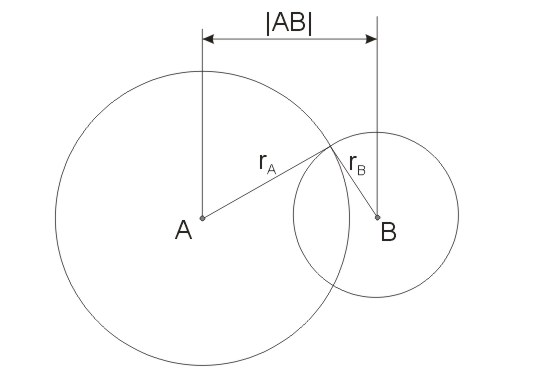
Okręgi przecinające się zostały zilustrowane na poniższym rysunku. Oba okręgu mają dwa punkty wspólne. Jeżeli dane są promienie i środki dwóch okręgów, to dla okręgów przecinających się prawdziwa jest nierówność \(r_a-r_b<|AB|<r_a+r_b\).

Okręgi przecinające się

Okręgi wewnętrznie styczne

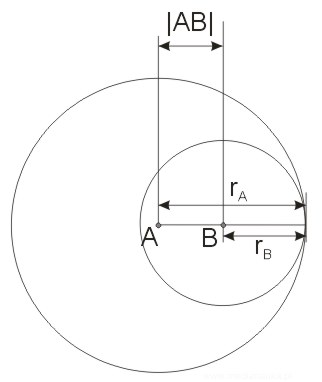
Okręgi wewnętrznie styczne zostały zilustrowane na poniższym rysunku. Oba okręgu mają jeden punkt wspólny, a pozostałe punkty jednego z okręgów leżą wewnątrz drugiego okręgu. Jeżeli dane są promienie i środki dwóch okręgów, to dla okręgów wewnętrznie stycznych prawdziwa jest równość \(r_a-r_b=|AB|\).

Okręgi wewnętrznie styczne

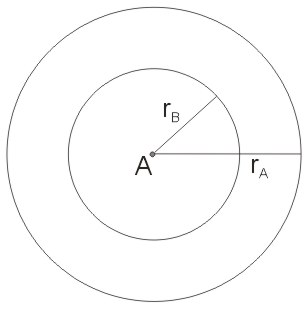
Jeden okrąg leży wewnątrz drugiego

Ten przypadek został zilustrowany na poniższym rysunku. Oba okręgu nie mają punktów wspólnych, a wszystkie punkty jednego z okręgów leżą wewnątrz drugiego okręgu. Jeżeli dane są promienie i środki dwóch okręgów, to dla tego przypadku prawdziwa jest nierówność \(r_a-r_b>|AB|\).

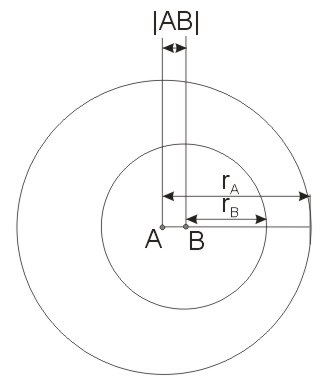
ilustracja

Okręgi współśrodkowe

Okręgi współśrodkowe zostały zilustrowane na poniższym rysunku. Oba okręgu nie mają punktów wspólnych, wszystkie punkty jednego z okręgów leżą wewnątrz drugiego okręgu. Oba okręgi mają wspólne środki. Okręgi współśrodkowe są szczególnym przypadkiem leżenia okręgu wewnątrz drugiego.

Okręgu współśrodkowe

Powiązane materiały

Okrąg i koło

Równanie okręgu

Liczba pi

Pole koła i długość okręgu