Nierówności
Nierówność z jedną niewiadomą jest to jedna z następujących form zdaniowych:
\(f(x)<g(x)\)
\({f(x)>g(x)}\)
\({f(x)\geq{g(x)}}\)
\({f(x)\leq{g(x)}}\)
gdzie \(f, g\) oznaczają funkcje zmiennej rzeczywistej. Zmienną \(x\) nazywamy niewiadomą. Pierwsze dwie nierówności nazywamy ostrymi, ostatnie dwie — nieostrymi.
Przykłady nierówności
Oto kilka przykładów nierówności:
- \(x<5\)
- \(x+1\geq{0}\)
- \(-x+1>2x+44\)
- \(\sqrt{x}+1\leq \sin{x}\)
- \(\frac{x^4-\sqrt{\frac{1}{x^2+1}}}{\log_2{(1+x^2)}}+1\geq \sin{(x-\sqrt{1+2x})}\)
- \(m^2+m>2m-1\)
Znak nierówności
Wyróżniamy nierówności ostre i nieostre.
Znakami nierówności ostrych są:
- „<” — „mniejsze od”,
- „>” — „większe od”.
Znakami nierówności nieostrych są:
- „\(\leq\)” — „mniejsze lub równe od”,
- „\(\geq\)” — „większe lub równe od”.
Dziedzina nierówności
Dziedzina nierówności jest to część wspólna dziedzin funkcji \(f, g\).
Przykłady
Jaka jest dziedzina nierówności \(\frac{2}{x+1}<\frac{1}{x}\)?
Dziedziną \(\frac{2}{x+1}\) jest \(\mathbb{R}\setminus \lbrace-1\rbrace\), a wyrażenia \(\frac{1}{x}\) jest zbiór \(\mathbb{R}\setminus \lbrace 0\rbrace\). Zatem dziedziną tej nierówności jest zbiór \(\mathbb{R}\setminus \lbrace -1,0\rbrace\).
Rozwiązywanie nierówności
Rozwiązanie nierówności jest to każda liczba, która spełnia tę nierówność. Co to oznacza? Jeżeli dowolną liczbę, która jest rozwiązaniem nierówności, podstawimy za niewiadomą, to otrzymamy zdanie prawdziwe.
Zbiór rozwiązań nierówności jest to zbiór utworzony ze wszystkich rozwiązań tej nierówności.
Aby rozwiązać nierówność, należy znaleźć jej zbiór rozwiązań. Rozwiązanie nierówności najlepiej jest przedstawiać w postaci przedziału liczbowego.
Jeżeli nierówność nie ma rozwiązań (zbiorem rozwiązań jest zbiór pusty), to nazywamy ją sprzeczną.
Nierówności równoważne
Nierówności są równoważne, jeżeli mają ten sam zbiór rozwiązań.
Przykłady
Przykład nierówności równoważnych:
- \(x+1>2\)
- \(x-1>0\)
Przykład nierówności sprzecznych:
- \(x^2<0\)
- \(x+1>x+2\)
Przykłady
Rozwiąż nierówność \(-2x+4>0\).
Przekształcamy naszą nierówność do postaci nierówności równoważnych:
Najpierw przenosimy liczbę 4 na drugą stronę nierówności, zmieniając jej znak:
\(-2x>-4\)
Dzielimy obie strony nierówności przez \((-2)\), a ponieważ dzielimy przez liczbę ujemną, zmieniamy znak nierówności na przeciwny.
\(-2x>-4/:(-2)\)
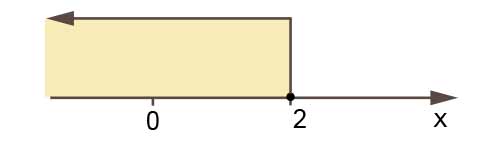
\(x<2\)
Rozwiązaniem nierówności są liczby rzeczywiste mniejsze od dwóch. Możemy to przedstawić za pomocą przedziału: \(x\in (-\infty; 2)\) lub wykresu na osi liczbowej.
Pytania
Jak sprawdzić, czy podana liczba spełnia nierówność?
Aby sprawdzić, czy podana liczba spełnia nierówność, należy podstawić za niewiadomą tę właśnie liczbę i sprawdzić, czy nierówność jest prawdziwa.
Na przykład, aby sprawdzić, czy liczba \(1\) spełnia nierówność \(x-4>0\), obliczamy \(1-4>0\), co daje nam zdanie fałszywe \(-3>0\). Liczba \(1\) nie spełnia więc naszej nierówności.
Jak rozwiązywać nierówności?
Stosujemy pewne metody rozwiązywania nierówności. Poniżej przedstawiamy linki do artykułów, w których pokazujemy, jak rozwiązujemy różne typy nierówności:
- Jak rozwiązywać nierówności liniowe?
- Jak rozwiązywać nierówności kwadratowe?
- Jak rozwiązywać nierówności algebraiczne?
- Jak rozwiązywać nierówności wykładnicze?
- Jak rozwiązywać nierówności logarytmiczne?
- Jak rozwiązywać nierówności trygonometryczne?
- Metoda nierówności równoważnych.
Kiedy zmieniamy znak nierówności?
Zawsze zmieniamy znak nierówności na przeciwny, gdy mnożymy lub dzielimy obie strony nierówności przez liczbę ujemną.
Jak rozwiązywać nierówności z wartością bezwzględną.
Temu zagadnieniu poświęcamy odrębny artykuł, do którego link znajdziesz poniżej.
Zadania z rozwiązaniami

Zadanie nr 1 — maturalne.
Jedną z liczb, które spełniają nierówność \(-x^5+x^3-x<-2\) jest:
A. \(1\)
B. \((-1)\)
C. \(2\)
D. \((-2)\)

Zadanie nr 2 — maturalne.
Do zbioru rozwiązań nierówności \((x^4+1)(2-x)>0\) nie należy:
A. \((-3)\)
B. \((-1)\)
C. \(1\)
D. \(3\)

Zadanie nr 3 — maturalne.
Udowodnij, że dla dowolnych liczb dodatnich \(a\), \(b\) prawdziwa jest nierówność.
\(\frac{1}{2a}+\frac{1}{2b}\geq \frac{2}{a+b}\)

Zadanie nr 4 — maturalne.
Udowodnij, że dla dowolnych dodatnich liczb rzeczywistych \(x\) i \(y\), takich że \(x<y\) , i dowolnej dodatniej liczby rzeczywistej \(a\) prawdziwa jest nierówność:
\(\frac{x+a}{y+a}+\frac{y}{x}>2\)

Zadanie nr 5 — maturalne.
Zbiorem wszystkich rozwiązań nierówności \(3(1−x)>2(3x−1)−12x\) jest przedział
A. \((-\frac{5}{3},+\infty)\)
B. \((-\infty,\frac{5}{3})\)
C. \((\frac{5}{3},+\infty)\)
D. \((-\infty,-\frac{5}{3})\)

Zadanie nr 6 — maturalne.
Zbiorem wszystkich rozwiązań nierówności \(\frac{2}{5}-\frac{x}{3}>\frac{x}{5}\) jest przedział
A. \((-\infty; 0)\)
B. \((0; +\infty)\)
C. \((-\infty; \frac{3}{4})\)
D. \((\frac{3}{4}; +\infty)\)
Powiązane materiały
© medianauka.pl, 2009-06-22, A-239
Data aktualizacji artykułu: 2023-05-01

 Równanie
Równanie Rozwiązywanie równań
Rozwiązywanie równań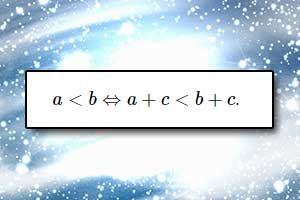 Rozwiązywanie nierówności
Rozwiązywanie nierówności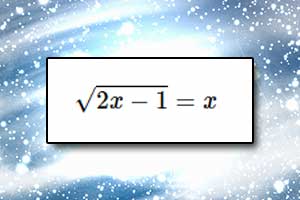 Metoda analizy starożytnych
Metoda analizy starożytnych Równania i nierówności — podstawy
Równania i nierówności — podstawy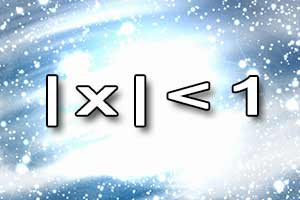 Nierówności z wartością bezwzględną
Nierówności z wartością bezwzględną