Nierówność logarytmiczna

Nierówność logarytmiczna to taka nierówność, w której niewiadoma jest w podstawie logarytmu lub pod znakiem logarytmu.

Przykład

Poniżej kilka przykładów nierówności logarytmicznych.

$\log_{x}{5}>3\\{\log_{5}{x}<3}\\{\log_{\frac{x}{2}}{x}\geq{2}}$

Rozwiązywanie nierówności logarytmicznych

Rozwiązywanie nierówności logarytmicznych wymaga najpierw określenia dziedziny nierówności, czyli wszystkich wartości x, dla których nierówność (w tym logarytm) ma sens matematyczny. Rozwiązań szukamy w tym właśnie zbiorze.

Przy rozwiązywaniu nierówności logarytmicznych korzystamy z monotoniczności funkcji logarytmicznej.

Jeżeli podstawa logarytmu a>1, to funkcja logarytmiczna jest rosnąca i nierówności argumentów odpowiada taka sama nierówność wartości funkcji.

$\log_{a}{x}<\log_{a}{y}\Leftrightarrow{x<y}$

Przykład

Rozwiąż nierówność logarytmiczną: $\log_{2}{x}\leq{4}$

Najpierw określamy dziedzinę nierówności. Liczba logarytmowana musi być większa od zera. Mamy więc warunek x>0.

Teraz liczbę 4 należy wyrazić poprzez logarytm o podstawie 2 (4=log₂16) i ponieważ podstawa logarytmów jest większa od jedności, nierówność wartości funkcji możemy zastąpić nierównością jej argumentów, bez konieczności zmiany zwrotu nierówności.

$\log_{2}{x}\leq{4}\\{\log_{2}{x}\leq{\log_{2}{16}}\\x\leq{16}$

Zaznaczamy na osi liczbowej dziedzinę nierówności oraz otrzymany wynik i wyznaczamy część wspólną zbiorów. Jest to rozwiązanie naszej nierówności.

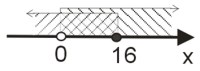
Odpowiedź: $x\in(0;16\rangle$

Jeżeli podstawa logarytmu 0<a<1, to funkcja logarytmiczna jest malejąca i nierówności argumentów odpowiada nierówność wartości funkcji o przeciwnym zwrocie.

$\log_{a}{x}<\log_{a}{y}\Leftrightarrow{x>y}$

Przykład

Rozwiązać nierówność: $\log_{\frac{1}{2}}{x}\leq{0}$

Określamy dziedzinę nierówności. Liczba logarytmowana musi być większa od zera. Mamy więc warunek x>0.
Teraz liczbę 0 należy wyrazić poprzez logarytm o podstawie 1/2 (0=log_1/21) i ponieważ podstawa logarytmów jest mniejsza od jedności, nierówność wartości funkcji możemy zastąpić nierównością jej argumentów, ale wymagana jest zmiana zwrotu nierówności.

$\log_{\frac{1}{2}}{x}\leq{0}\\{\log_{\frac{1}{2}}{x}\leq{\log_{\frac{1}{2}}{1}}}\\x\geq{1}$
Wszystkie rozwiązania należą do dziedziny nierówności.
Odpowiedź: $x\in{\langle1;+\infty)}$

W osobnym artykule pokazujemy jak rozwiązujemy równania logarytmiczne.

Zadania z rozwiązaniami

Zadania związane z tematem:
Nierówność logarytmiczna

Zadanie - nierówność logarytmiczna
Rozwiązać nierówność logarytmiczną $\log_{\frac{1}{3}}{x^2}\geq 1$

Pokaż rozwiązanie zadania

Zadanie - rozwiązać nierówność logarytmiczną
Rozwiązać nierówność logarytmiczną $\log_{x}{3}<0$

Pokaż rozwiązanie zadania

Zadanie - rozwiązać nierówność logarytmiczną
Rozwiązać nierówność logarytmiczną $\frac{4\log_{\frac{1}{2}}{x}}{1+\log_{\frac{1}{2}{x}}}\geq 2$

Pokaż rozwiązanie zadania

Zadanie - nierówność logarytmiczna
Rozwiązać nierówność logarytmiczną $\log_{3}{x}+\log_{9}{x}\leq \log_{\frac{1}{3}}{\sqrt{5}}$

Pokaż rozwiązanie zadania

Zadanie - nierówność logarytmiczna
Rozwiązać nierówność logarytmiczną $\log_{\frac{2}{x+1}}{\frac{1}{3}}>0$

Pokaż rozwiązanie zadania

Zadanie - nierówność wykładnicza
Rozwiązać nierówność wykładniczą $\frac{5^x}{5}\leq 7$ .

Pokaż rozwiązanie zadania

Test wiedzy

Sprawdź swoje umiejętności z materiału zawartego w tej lekcji.

Nierówność logarytmiczna

Rozwiązywanie nierówności logarytmicznych

Zadania z rozwiązaniami

Polecamy w naszym sklepie