Równania logarytmiczne
Równanie logarytmiczne to takie równanie, w którym niewiadoma jest w podstawie logarytmu lub pod znakiem logarytmu.
Przykłady równań logarytmicznych
Oto proste równania logarytmiczne:
- \(\log_{x}{5}=3\)
- \(\log_{5}{x}=3\)
- \(\log_{\frac{x}{2}}{x}=2\)
Rozwiązywanie równań logarytmicznych wymaga najpierw określenia dziedziny równania, czyli wszystkich wartości \(x\), dla których równanie (w tym logarytm) ma sens matematyczny. Rozwiązań szukamy w tym właśnie zbiorze. Można stosować co najmniej kilka metod rozwiązywania równań logarytmicznych. Tutaj zostaną przedstawione dwie najczęściej stosowane.
Rozwiązywanie równań logarytmicznych na podstawie definicji logarytmu
Metodę najlepiej przedstawić na przykładzie.
Przykład 1
Rozwiąż równanie logarytmiczne \(\log_{x}{9}=2\).
Określmy dziedzinę równania. Z definicji logarytmu wiemy, że podstawa logarytmu musi być większa od zera i różna od jedności. Mamy więc warunek:
\(\begin{cases}x>0\\x\neq{1}\end{cases}\)
Teraz skorzystamy bezpośrednio z definicji logarytmu:
\(\log_{x}{9}=2\Leftrightarrow{x^2=9}\)
Dalej już rozwiązujemy zwykłe równanie kwadratowe.
\(x^2=9\)
\(x^2-9=0\)
\((x-3)(x+3)=0\)
\(x_1=-3,x_2=3\)
Sprawdzamy teraz, czy rozwiązania należą do dziedziny równania. W tym przypadku tylko drugi pierwiastek spełnia równanie.
Odpowiedź: \(x=3\).
Metoda podstawienia
Jeżeli w równaniu powtarza się ten sam logarytm, można go zastąpić nową zmienną i rozwiązać równanie względem tej zmiennej.
Przykład 2
Rozwiąż równanie logarytmiczne:
\(\frac{1}{\log_{2}{x}}=\log_{2}{x}\)
Równanie (logarytm) ma sens dla dodatnich wartości \(x\) - jest to nasza dziedzina równania.
W powyższym równaniu zastosujemy podstawienie \(t=\log_{2}{x}\).
\(\frac{1}{t}=t\)
\(\frac{1}{t}-t=0\)
\(\frac{1-t^2}{t}=0\)
\(1-t^2=0/\cdot(-1)\)
\(t^2-1=0\\(t-1)(t+1)=0\)
\(t_1=1,\quad{}t_2=-1\)
Za zmienną \(t\) podstawiamy \(\log_{2}{x}\).
Mamy więc:
\(\log_{2}{x_1}=1,\quad{}\log_{2}{x_2}=-1\)
Korzystamy teraz z definicji logarytmu i otrzymujemy:
\(2^1=x_1,\quad{}2^{-1}=x_2\)
\(x_1=2,\quad{}x_2=\frac{1}{2}\)
Oba rozwiązania należą do dziedziny równania, są więc rozwiązaniem równania \(\frac{1}{\log_{2}{x}}=\log_{2}{x}\).
W osobnym artykule pokazujemy jak rozwiązujemy nierówności logarytmiczne oraz równania wykładnicze.
Zadania z rozwiązaniami

Zadanie nr 5.
Rozwiązać równanie logarytmiczne \(\log_{4}{[\log_{2}{(x-4)}]}=2\).

Zadanie nr 6.
Rozwiązać równanie logarytmiczne \(\log_{3}{(1-x)}=\log_{3}{(x-3)}+2\).

Zadanie nr 7.
Rozwiązać równanie logarytmiczne \(\log_{\frac{1}{3}}{(x+2)}+\log_{3}{(x+3)}+1=0\).

Zadanie nr 8.
Rozwiązać równanie logarytmiczne \(\frac{2}{\log{x}+1}-\frac{1}{\log{x}-1}=0\).
Powiązane materiały
© medianauka.pl, 2009-12-10, A-424
Data aktualizacji artykułu: 2023-05-09

 Równanie logarytmiczne
Równanie logarytmiczne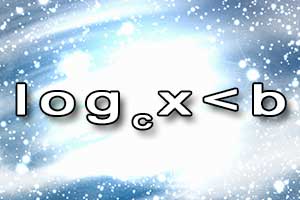 Nierówność logarytmiczna
Nierówność logarytmiczna