Nierówność kwadratowa

Definicja

$ax^2+bx+c<0\\ax^2+bx+c>0\\ax^2+bx+c\leq{0}\\ax^2+bx+c\geq{0}$

gdzie $a\neq{0}$ , b, c - są dowolnymi liczbami rzeczywistymi, nazywamy nierównością kwadratową lub nierównością drugiego stopnia.

Przykład

Kilka przykładów nierówności kwadratowych:
$-x^2-2x+5<0\\5x^2+3\leq{0}\\-3x^2-x\geq{0}$

Rozwiązywanie nierówności kwadratowych

Rozwiązywanie nierówności kwadratowej najłatwiej oprzeć o wykresy zmienności trójmianu kwadratowego. Wszystkie możliwości zmienności wykresu trójmianu kwadratowego w zależności od współczynnika a oraz wyróżnika trójmianu kwadratowego zostały pokazane na poniższym schemacie:

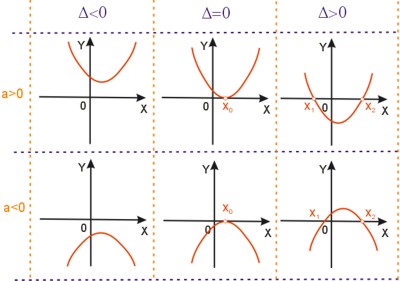
wykres trójmianu kwadraowego

Przypomnijmy sobie jeszcze tylko oznaczenia:

$\Delta=b^2-4ac\\{x_1=\frac{-b-\sqrt{\Delta}}{2a},\quad{x_2=\frac{-b+\sqrt{\Delta}}{2a}}}\\x_0=-\frac{b}{2a}$

Skorzystajmy zatem z powyższych informacji przy rozwiązywaniu prostych nierówności.

Zadanie

Rozwiązać nierówność kwadratową

$a=1\\b=3\\c=-4$
Obliczamy wyróżnik
$\Delta=b^2-4ac=3^2-4\cdot{1}\cdot(-4)=9+16=25$
Wyróżnik jest większy od zera, więc trójmian ma dwa pierwiastki.
$\sqrt{\Delta}=5$
$x_1=\frac{-b-\sqrt{\Delta}}{2a}=\frac{-3-5}{2}=-4\\{x_2=\frac{-b+\sqrt{\Delta}}{2a}=\frac{-3+5}{2}=1}$

Wyróżnik jest większy od zera, współczynnik a również, więc wykres trójmianu przecina oś OX w dwóch miejscach, a ramiona paraboli skierowane są w górę (spójrzmy na trzeci wykres na powyższym rysunku). Interesują nas wartości mniejsze od zera, więc dotyczy to wszystkich argumentów z przedziału (x₁;x₂) - nierówność jest ostra, więc przedział jest otwarty.
Warto zawsze naszkicować schemat wykresu, z którego odczytujemy rozwiązanie.

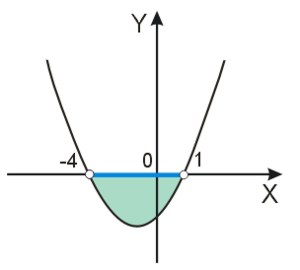
Odpowiedź: $x\in(-4;1)$

Zadanie

Rozwiązać nierówności kwadratowe:

$-x^2+6x-9>0,\\-x^2+6x-9<0,\\-x^2+6x-9\geq{0},\\-x^2+6x-9\leq{0}$

$a=-1\\b=6\\c=-9$
Obliczamy wyróżnik
$\Delta=b^2-4ac=6^2-4\cdot(-1)\cdot(-9)=36-36=0$

Wyróżnik jest równy zero, więc trójmian ma jeden podwójny pierwiastek, współczynnik a jest ujemny, więc ramiona paraboli są skierowane w dół. Z wykresu odczytamy więc rozwiązania wszystkich nierówności.

$x_0=\frac{-b}{2a}=\frac{-6}{-2}=3$

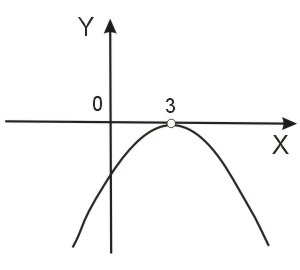
W przypadku nierówności żaden punkt wykresu nie leży nad osią OX, nierówność więc nie ma rozwiązania - jest sprzeczna.
W przypadku nierówności wszystkie punkty wykresu z wyjątkiem (3,0) leżą pod osią OX, rozwiązaniem nierówności jest zbiór $(-\infty;3)\cup(3;\infty)$
W przypadku nierówności $-x^2+6x-9\geq{0}$ tylko jedna liczba spełnia tę nierówność:
W przypadku nierówności $-x^2+6x-9\leq{0}$ wszystkie punkty wykresu leżą pod lub na osi OX, więc rozwiązaniem nierówności jest zbiór (nierówność jest tożsamościowa).

Zadania z rozwiązaniami

Zadania związane z tematem:
Nierówność kwadratowa

Zadanie - nierówność kwadratowa, właściwości pierwiastka, nierówność z parametrem
Dla jakiej wartości parametru x prawdziwa jest równość $\sqrt{(x^2-2x+1)^2}=x^2-2x+1$ ?

Pokaż rozwiązanie zadania

Zadanie - nierówność kwadratowa z wartością bezwzględną
Rozwiązać nierówność $2x^2-|x+1|\leq -1$

Pokaż rozwiązanie zadania

Zadanie - nierówność kwadratowa
Rozwiązać nierówność:
a) $x^2+2x-3\geq 0$
b) $-x^2+\frac{3}{4}x-\frac{1}{8}> 0$
c) $-x^2+2\leq 0$

Pokaż rozwiązanie zadania

Zadanie - nierówność kwadratowa
Rozwiązać nierówność:
a) $\sqrt{3}x^2+\sqrt{2}x+1< 0$
b) $-x^2-2x-5\geq 0$

Pokaż rozwiązanie zadania

Zadanie - nierówność kwadratowa
Rozwiązać nierówność:
a)
b) $-x^2+2\sqrt{2}x-2\geq 0$

Pokaż rozwiązanie zadania

Zadanie - nierówność kwadratowa z parametrem
Dla jakich wartości parametru m nierówność $x^2-2x-m+1\leq 0$ ma jedno rozwiązanie x=1?

Pokaż rozwiązanie zadania

Zadanie - nierówność kwadratowa z parametrem
Dla jakich wartości parametru m zbiorem rozwiązań nierówności jest:
a) zbiór liczb rzeczywistych
b) zbiór pusty ?

Pokaż rozwiązanie zadania

Zadanie - nierówność kwadratowa
Rozwiązać nierówność $\frac{x}{x+1}\geq 2$

Pokaż rozwiązanie zadania

Zadanie maturalne nr 27, matura 2016 (poziom podstawowy)
Rozwiązać nierówność .

Pokaż rozwiązanie zadania

Zadanie maturalne nr 26, matura 2015 (poziom podstawowy)
Rozwiąż nierówność 2x²-4x>(x+3)(x-2).

Pokaż rozwiązanie zadania

Zadanie - dziedzina funkcji logarytmicznej
Wyznaczyć dziedzinę funkcji $y=\log(5x^2-3x+1)$

Pokaż rozwiązanie zadania

Inne zagadnienia z tej lekcji

Test wiedzy