Nierówność z wartością bezwzględną
Rozwiązanie nierówności z wartością bezwzględną wymaga zastosowanie własności wynikającej bezpośrednio z definicji wartości bezwzględnej.
Rozwiązania nierówności z wartością bezwzględną
Dla każdej liczby rzeczywistej \(a>0\):
\(|x|<a \Leftrightarrow -a<x<a\)
\(|x|>a \Leftrightarrow [(x<-a) \vee (x>a)]\)
Powyższe można zapisać w postaci przedziałów liczbowych:
\(|x|<a \Leftrightarrow x\in (-a,a)\)
\(|x|>a \Leftrightarrow x\in(-\infty;-a) \cup (a;+\infty)\)
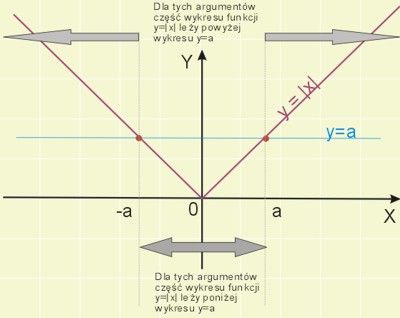
Interpretacja geometryczna
Interpretacja geometryczna nierówności zilustrowana została na rysunku.
Przykład 1
Rozwiąż nierówność z wartością bezwzględną:
\(|x+2|<4\)
\(|x+2|<4 \Leftrightarrow {-4<x+2<4} \Leftrightarrow {-6<x<2}\)
Powyższe rozwiązanie można zapisać w postaci przedziału \(x\in (-6;2)\).
Przykład 2
Rozwiązać nierówność: \(|x-2|>2\).
\(|x-2|>2 \Leftrightarrow [(x-2<-2) \vee (x-2>2)] \Leftrightarrow [(x<0) \vee (x>4)]\)
Zapiszmy jeszcze powyższe rozwiązanie w postaci przedziału \(x\in (-\infty;0)\cup (4;\infty)\).
Jak zauważamy cała sztuka rozwiązania nierówności pierwszego stopnia z wartością bezwzględną polega na wykorzystaniu definicji wartości bezwzględnej i umiejętności zapisywania wyniku w postaci przedziałów liczbowych.
Rozwiązywanie nierówności z wartością bezwzględną
Zamiast korzystać z powyższych wzorów, można dowolną nierówność z jedną lub wieloma wartościami bezwzględnymi rozwiązać z wykorzystaniem wprost definicji wartości bezwzględnej.
Rozpatrujemy wówczas wszystkie przypadki, w których wyrażenie pod wartością bezwzględną jest nieujemne i ujemne.
Jeżeli wyrażenie to jest większe lub równe zero, to opuszczamy symbol wartości bezwzględnej, dalej rozwiązując nierówność w tradycyjny sposób.
Jeżeli wyrażenie to jest ujemne, również opuszczamy symbol wartości bezwzględnej, ale wówczas zmieniamy znak tego wyrażenia na przeciwny.
Na końcu uwzględniamy wszystkie uzyskane wyniki, określając przedziały, w których nasza nierówność jest prawdziwa. Postępujemy więc w sposób analogiczny, jak w przypadku rozwiązywania równań z wartością bezwzględną.
Zadania z rozwiązaniami
Zadanie nr 2 — maturalne.
Rozwiąż nierówność:
\(\sqrt{x^2+4x+4}<\frac{25}{3}-\sqrt{x^2-6x+9}\)
Zapisz obliczenia. Wskazówka: skorzystaj z tego, że \(\sqrt{a^2}=|a|\) dla każdej liczby rzeczywistej \(a\).
Powiązane materiały
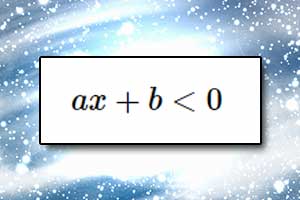Nierówność liniowa z jedną niewiadomą
Rozwiązywanie nierówności
Wartość bezwzględna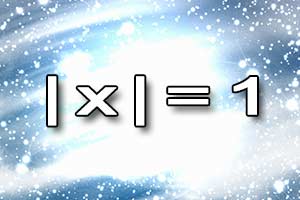
Równania z wartością bezwzględną© medianauka.pl, 2009-06-27, A-250
Data aktualizacji artykułu: 2023-05-03