Równania z wartością bezwzględną
Równania z wartością bezwzględną to takie równania, w których niewiadoma znajduje się pod wartością bezwzględną. Tutaj zajmiemy się wyłącznie równaniami pierwszego stopnia.
Rozwiązywanie równań z wartością bezwzględną
Rozwiązywanie równania z wartością bezwzględną wymaga rozpatrywania kilku przypadków. Wynika to bezpośrednio z definicji wartości bezwzględnej.
Zgodnie z definicją:
Należy więc rozpatrzyć co najmniej dwa przypadki.
Przykład 1
Rozwiązać równanie: \(|x|-1=0\).
1) Dla \(x\geq{0}\) mamy \(|x|=x\), więc:
\(|x|-1=0\Rightarrow{x-1=0}\Leftrightarrow{x=1}\)
Spełnione jest założenie, więc liczba 1 jest pierwiastkiem równania.
2) Dla \(x<0\) mamy z definicji wartości bezwzględnej \(|x|=-x\), więc:
\(|x|-1=0\Rightarrow{-x-1=0}\Leftrightarrow{x=-1}\)
Spełnione jest założenie (\(x<0\)), więc liczba \(-1\) jest pierwiastkiem równania.
Odpowiedź: Pierwiastkami równania \(|x|-1=0\) są liczby \(-1\) i \(1\).
Naszkicujmy wykres funkcji \(y=|x|-1\).
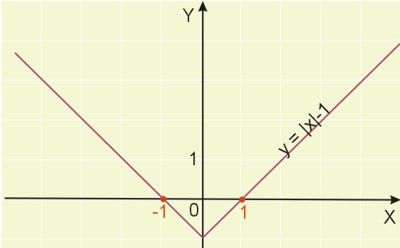
Jak widać, wykres tej funkcji ma dwa miejsca zerowe, są to jednocześnie pierwiastki rozpatrywanego równania.
Przykład 2
Rozwiązać równanie: \(|x|+1=0\).
1) Dla \(x\geq{0}\) mamy \(|x|=x\), więc:
\(x+1=0\)
\(x=-1\)
Niestety nie jest spełnione założenie \(x\geq{0}\), więc liczba -1 nie jest pierwiastkiem równania.
2) Dla \(x<0\) mamy z definicji wartości bezwzględnej \(|x|=-x\), więc:
\(-x+1=0\)
\(x=1\)
Nie jest spełnione założenie (\(x<0\)), więc liczba 1 nie jest pierwiastkiem równania.
Odpowiedź: Równanie nie ma rozwiązań; jest sprzeczne.
Naszkicujmy wykres funkcji \(y=|x|+1\).
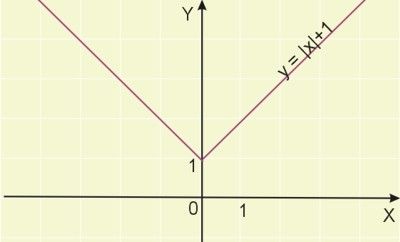
Jak się należało spodziewać, wykres tej funkcji nie ma miejsc zerowych.
W przypadku gdy pod wartością bezwzględną znajduje się całe wyrażenie zawierające zmienną, rozpatrujemy przypadki, gdy całe to wyrażenie przyjmuje różne znaki. Ilustruje to poniższy przykład.
Przykład 3
Rozwiązać równanie: \(|x+1|+x=1\)
1) Dla \(x+1\geq{0}\Leftrightarrow{x\geq{-1}}\) otrzymujemy równanie:
\(x+1+x=1\)
\(2x=0\)
\(x=0\)
2) Dla \(x+1<0\Leftrightarrow{x<-1}\) otrzymujemy równanie:
\(-x-1+x=1\)
\(-1=1\)
Otrzymaliśmy sprzeczność.
Odpowiedź: Równanie ma jeden pierwiastek \(x=0\).
Równanie z dwiema wartościami bezwzględnymi
Jeżeli w równaniu pojawia się więcej wartości bezwzględnych, np. \(|x+1|-x=|x|-1\), wówczas musimy rozpatrywać odpowiednio więcej przypadków (kiedy obie wartości pod wartościami bezwzględnymi są ujemne, obie dodatnie oraz jedna z nich dodatnia, druga ujemna i odwrotnie). Poniżej zamieszczamy kilka zadań z rozwiązaniami, na których przykładach można prześledzić proces rozwiązywania takich równań.
Zadania z rozwiązaniami
Zadanie nr 6 — maturalne.
Dana jest funkcja \(f\) określona wzorem
\(f(x)=\begin{cases}x-2 \quad dla \quad x\leq0\\||x+3|-4| \quad dla \quad x>0 \end{cases}\).
Równanie \(f(x)=1\) ma dokładnie
A. jedno rozwiązanie.
B. dwa rozwiązania.
C. cztery rozwiązania.
D. pięć rozwiązań.
Zadanie nr 8 — maturalne.
Wyznacz wszystkie wartości parametru \(a\), dla których równanie \(|x−5|=(a−1)^2−4\) ma dwa różne rozwiązania dodatnie.
Zadanie nr 9 — maturalne.
Liczba różnych pierwiastków równania \(3x+|x-4|=0\) jest równa
A. 0
B. 1
C. 2
D. 3
Zadanie nr 11.
Dany jest wektor \(\vec{AB}=[2,5]\) zaczepiony w punkcie \(A=(1,1)\). Znaleźć taki punkt \(C\), leżący na prostej \(y=2\), że pole trójkąta \(ABC\) jest równe 10.
Powiązane materiały
Równanie liniowe
Równania liniowe
Wartość bezwzględna
Nierówności z wartością bezwzględną© medianauka.pl, 2009-06-26, A-249
Data aktualizacji artykułu: 2023-05-03