Nierówność liniowa
Nierówność liniowa z jedną niewiadomą jest to nierówność:
\(ax+b<0\)
\(ax+b>0\)
\(ax+b\leq 0\)
\( ax+b\geq 0\)
gdzie \(a\) i \(b\) — dowolne liczby rzeczywiste, \(x\) — niewiadoma.
Przykłady
Przykłady nierówności liniowych:
- \(2x-1\geq{0}\)
- \(\frac{x}{3}-1\leq 0\)
- \(-x+\sqrt{3}<0\)
Rozwiązania nierówności liniowej
Jeżeli \(a\neq{0}\), to nierówność liniową nazywamy nierównością pierwszego stopnia.
W zależności rodzaju nierówności zbiorem rozwiązań są przedziały:
\((-\infty;-\frac{b}{a}), (-\frac{b}{a};+\infty)\) dla ostrych nierówności
lub
\((-\infty;-\frac{b}{a}\rangle,\langle-\frac{b}{a};+\infty)\) dla nierówności nieostrych.
Jeżeli \(a=0\), to nierówność liniowa jest tożsamościowa (np. \(-2<3\)) lub sprzeczna (np. \(3<-2\)) w zależności od rodzaju i kierunku nierówności oraz wartości liczby b.
Przykłady
Przyjrzyjmy się na przykładzie nierówności \(2x-4>0\) i jej interpretacji geometrycznej.
Rozwiązujemy nierówność:
\(2x-4>0\)
\(2x>4/:2\)
\(x>2\)
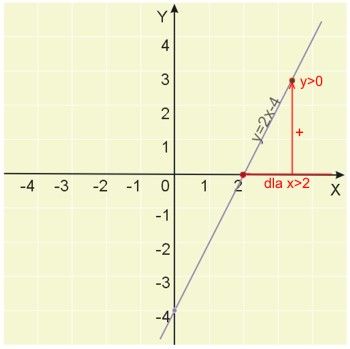
Przyjrzyjmy się wykresowi funkcji \(y=2x-4\).
Ponieważ rozpatrujemy \(y=2x-4>0\), więc pytamy: "dla jakich wartości zmiennej \(x\) wartości funkcji \(y\) są większe od zera?" i uzyskujemy odpowiedź: dla \(x>2\).
Widać to doskonale na zamieszczonej poniżej ilustracji.
Nierówności z jedną niewiadomą występują także w zadaniach z treścią, których przykłady również pokażemy.
Rozwiązywanie nierówności liniowych
Poniżej prosty przykład rozwiązania nierówności pierwszego stopnia z jedną niewiadomą.
Rozwiązać nierówność: \(\frac{5}{8}-\frac{3x}{2}\leq{1}\)
Rozwiązanie:
\(\frac{5}{8}-\frac{3x}{2}\leq{1}\)
\(-\frac{3}{2}x\leq{1}-\frac{5}{8}\)
\(-\frac{3}{2}x\leq{\frac{3}{8}}/\cdot{(-\frac{2}{3})}\)
\(x\geq-\frac{3}{8}\cdot{\frac{2}{3}}\)
\(x\geq-\frac{1}{4}\)
Odpowiedź: \(x\in \langle-\frac{1}{4};+\infty)\).
Nierówności liniowe z parametrem
Nie zawsze w nierówności jawnie zapisywane są liczby. Zamiast nich stosuje się oznaczenia literowe, nazywane parametrami, a nierówność zawierająca takie oznaczenia literowe jest nazywana nierównością z parametrem. Zawsze w takim równaniu musimy wskazać niewiadomą lub ze względu na jaką zmienną należy rozwiązać daną nierówność.
Cel parametryzowania został omówiony przy okazji rozwiązywanie równań pierwszego stopnia.
Przykłady
Rozwiązać nierówność ze względu na niewiadomą \(x\).
\(mx-x-5\geq{0}\)
\((m-1)x\geq{5}\)
1) Jeżeli \(m=1\), wówczas nierówność jest sprzeczna ( \(0\cdot{x}\geq{5}\)).
2) Jeżeli \(m\neq{1}\quad{i}\quad{m-1>0}\) wówczas:
\((m-1)x\geq{5}/:(m-1)\)
\(x\geq{\frac{5}{m-1}}\)
3) Jeżeli \(m\neq{1}\quad{i}\quad{m-1<0}\) wówczas:
\((m-1)x\geq{5}/:(m-1)\)
\(x\leq{\frac{5}{m-1}}\)
Odpowiedź: Dla \(m=1\) nierówność nie ma rozwiązania, dla \(m>1\) zbiorem rozwiązań jest przedział \(\langle{\frac{5}{m-1}};+\infty)\), dla \(m<1\) zbiorem rozwiązań nierówności jest przedział \((-\infty;\frac{5}{m-1}\rangle\).
Na podstawie tego przykładu widać, że jeżeli mnożymy obie strony nierówności przez wyrażenie, co do znaku którego nie jesteśmy pewni, trzeba prowadzić często zawiłą analizę przypadków. Jeszcze gorzej jest w przypadku, gdy mnożymy obie strony nierówności przez zmienną. Należy unikać mnożenia stron nierówności przez wyrażenia zawierające niewiadomą.
Zadania z treścią
Osobną grupę zadań stanowią zadania z treścią. Najważniejsze w procesie rozwiązywania takich zadań jest dobre oznaczenie niewiadomej i zapisanie zdania logicznego wypowiadanego w treści zadania za pomocą nierówności.
Przykład
Paweł jest o 2 lata starszy od Piotrka. Kiedy suma wieku chłopców będzie większa od dziesięciokrotności różnicy wieku starszego chłopca i młodszego?
Niech \(x\) oznacza wiek Piotrka.
Wówczas \(x+2\) oznacza wiek Pawła.
Układamy nierówność: \(x+(x+2)>10(x+2-x)\) (rozpatrujemy przypadek, kiedy od wieku starszego chłopca odejmujemy wiek chłopca młodszego, w przeciwnym przypadku warunek jest zawsze spełniony).
\(2x+2>20\)
\( 2x>18 /:2\)
\( x>9\)
Odpowiedź: Warunek jest spełniony, gdy Piotr ma powyżej 9 lat, a Paweł powyżej 11 lat.
Zadania z rozwiązaniami
Zadanie nr 1.
Rozwiązać nierówność:
a) \(\frac{1}{2}(x-1)+x\geq 5-2(x+2)\)
b) \((x-5)^2\geq (x+4)^2\)
c) \(\frac{2x-3}{5}>\frac{1-x}{2}\)
Zadanie nr 2.
Rozwiązać nierówność \(x^2+ax<(x-a)^2\) ze względu na niewiadomą \(x\).
Zadanie nr 3.
W pewnej liczbie dwucyfrowej liczba jedności jest o 4 większa od liczby dziesiątek. Znaleźć tę liczbę, jeśli wiadomo, że jest większa od 40 i mniejsza od 50.
Zadanie nr 4.
Dziadek jest dwa razy starszy od wnuczka. Kiedy suma ich wieku przekroczy 90 lat?
Zadanie nr 5 — maturalne.
Ile liczb całkowitych x spełnia nierówność \(\frac{2}{7}<\frac{x}{14}<\frac{4}{3}\) ?
A. 14
B. 15
C. 16
D. 17
Zadanie nr 6 — maturalne.
Ile liczb całkowitych x spełnia nierówność \(\frac{2}{7}<\frac{x}{14}<\frac{4}{3}\) ?
A. 14
B. 15
C. 16
D. 17
Zadanie nr 7 — maturalne.
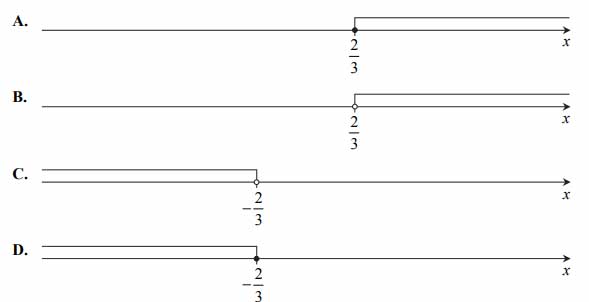
Wskaż rysunek, na którym jest przedstawiony zbiór wszystkich rozwiązań nierówności \(2-3x≥4\)
Zadanie nr 8 — maturalne.
Zbiorem wszystkich rozwiązań nierówności \(\frac{(1-2x)}{2}>\frac{1}{3}\) jest przedział:
- \((-\infty;\frac{1}{6})\)
- \((-\infty;\frac{2}{3})\)
- \((\frac{1}{6};+\infty)\)
- \((\frac{2}{3};+\infty)\)
Zadanie nr 9 — maturalne.
Zbiorem wszystkich rozwiązań nierówności \(\frac{(2-x)}{2}-2x\geq 1\) jest przedział
A. \(\langle 0, +\infty)\)
B. \((−\infty, 0\rangle\)
C. \((−\infty, 5\rangle\)
D. \((−\infty,\frac{1}{3}\rangle\)
Zadanie nr 10 — maturalne.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Zbiorem wszystkich rozwiązań nierówności \(-2(x+3)\leq \frac{2-x}{3}\) jest przedział
A. \((-\infty,-4]\)
B. \((-\infty,4]\)
C. \([-4,\infty)\)
D. \([4,\infty)\)
Inne zagadnienia z tej lekcji
Nierówności z wartością bezwzględną
Rozwiązywanie nierówności© medianauka.pl, 2009-06-25, A-247
Data aktualizacji artykułu: 2023-05-02