Nauka » Matematyka » Rozwiązywanie nierówności liniowych

Zadanie - nierówność liniowa

Rozwiązać nierówność:
a) $\frac{1}{2}(x-1)+x\geq 5-2(x+2)$
b) $(x-5)^2\geq (x+4)^2$
c) $\frac{2x-3}{5}>\frac{1-x}{2}$

a) Rozwiązanie zadania

W pierwszej kolejności pozbywamy się nawiasów po obu stronach nierówności. Następnie wyrazy z niewiadomą przenosimy na lewą stronę nierówności i pozostałe wyrazy na stronę prawą. Redukujemy wyrazy podobne i otrzymujemy wynik.

$\frac{1}{2}(x-1)+x\geq 5-2(x+2)\\ \frac{1}{2}x-\frac{1}{2}+x\geq 5-2x-4\\ \frac{1}{2}x+x+2x\geq \frac{1}{2}+1/\cdot 2\\ x+2x+4x\geq 1+2 \\ 7x\geq 3/:7 \\ x\geq \frac{3}{7}$

Wynik zapisujemy w postaci przedziału liczbowego.

Odpowiedź

$x\in \langle \frac{3}{7};+\infty)$

b) Rozwiązanie zadania

W pierwszej kolejności pozbywamy się nawiasów po obu stronach nierówności. Skorzystamy ze wzorów skróconego mnożenia:

$(a+b)^2=a^2+2ab+b^2\\ (a-b)^2=a^2-2ab+b^2$

Mamy więc:

$(x-5)^2\geq (x+4)^2\\ x^2-2\cdot x\cdot 5+5^2\geq x^2+2\cdot x\cdot 4+4^2\\ x^2-10x+25\geq x^2+8x+16$

Następnie wyrazy z niewiadomą przenosimy na lewą stronę nierówności i pozostałe wyrazy na stronę prawą. Redukujemy wyrazy podobne i otrzymujemy wynik.

$x^2-10x+25\geq x^2+8x+16\\ \cancel{x^2}-\cancel{x^2}-10x-8x\geq 16-25\\ -18x\geq -9/:(-18)\\ x\leq \frac{9}{18} \\ x\leq \frac{1}{2}$

Wynik zapisujemy w postaci przedziału liczbowego.

Odpowiedź

$x\in (-\infty;\frac{1}{2}\rangle$

c) Rozwiązanie zadania

W pierwszej kolejności pozbywamy się ułamków, mnożąc obie strony nierówności przez wspólny mianownik obu ułamków, a więc przez liczbę 10.

$\frac{2x-3}{5}>\frac{1-x}{2}/\cdot 10 \\ ^2 \cancel{10}\cdot \frac{2x-3}{\cancel{5}}> ^5\cancel{10}\cdot \frac{1-x}{\cancel{2}}\\ 2(2x-3)>5(1-x)$

Następnie pozbywamy się nawiasów i wyrazy z niewiadomą przenosimy na lewą stronę nierówności i pozostałe wyrazy na stronę prawą. Redukujemy wyrazy podobne i otrzymujemy wynik.

$2(2x-3)>5(1-x)\\ 4x-6>5-5x \\ 4x+5x>5+6 \\ 9x>11/:9 \\ x>\frac{11}{9}\\ x> 1\frac{2}{9}$

Wynik zapisujemy w postaci przedziału liczbowego:

Odpowiedź

$x\in (1\frac{2}{9};+\infty)$

Zadania podobne

Zadanie - nierówność liniowa z parametrem
Rozwiązać nierówność:

ze względu na niewiadomą x.

Pokaż rozwiązanie zadania

Zadanie - nierównośćliniowa - zadanie z treścią
W pewnej liczbie dwucyfrowej liczba jedności jest o 4 większa od liczby dziesiątek. Znaleźć tę liczbę, jeśli wiadomo, że jest większa od 40 i mniejsza od 50.

Pokaż rozwiązanie zadania

Zadanie - nierówności - zadanie z treścią
Dziadek jest dwa razy starszy od wnuczka. Kiedy suma ich wieku przekroczy 90 lat?

Pokaż rozwiązanie zadania

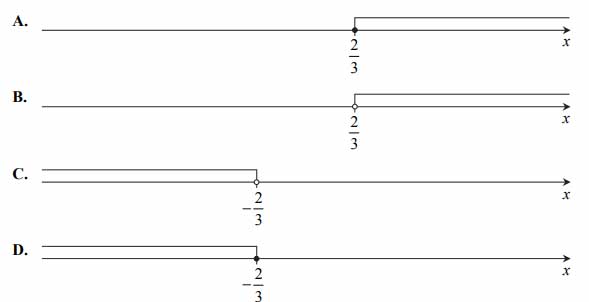
Zadanie maturalne nr 12, matura 2015 (poziom podstawowy)
Ile liczb całkowitych x spełnia nierówność $\frac{2}{7}< \frac{x}{14} < \frac{4}{3}$ ?

A. 14
B. 15
C. 16
D. 17

Pokaż rozwiązanie zadania