Rozwiązywanie nierówności
Jak rozwiązywać nierówności? Poznamy jedną z metod rozwiązywania nierówności.
Metoda nierówności równoważnych
Metoda nierówności równoważnych polega na ich przekształcaniu w taki sposób, aby każde kolejne było równoważne danej i łatwiejsze do rozwiązania. Możemy korzystać z następujących twierdzeń:
Twierdzenie
Dla każdego c prawdziwa jest równoważność: \(a<b \Leftrightarrow a+c<b+c\).
Podobne twierdzenia można sformułować dla pozostałych typów nierówności. Z powyższego twierdzenia wynika, że do obu stron nierówności możemy dodać dowolną liczbę (lub odjąć, czyli dodać liczbę przeciwną) lub całe wyrażenie i otrzymamy nierówność równoważną.
Przykład 1
Dana jest nierówność \(x+4>x^2+1\).
Jeżeli do obu stron nierówności dodamy liczbę \(-1\), to otrzymamy \(x+3>x^2\).
Otrzymaliśmy nierówność równoważną. Tak jak w przypadku równań możemy powiedzieć, że liczbę \(1\) z prawej strony nierówności przenosimy ze znakiem przeciwnym na lewą stronę.
Przykład 2
Rozwiązać nierówność: \(3x-3\leq 2x-3\).
Do obu stron nierówności dodajemy liczbę \(3\) (lub łatwiej powiedzieć: przenosimy liczbę \(3\) na drugą stronę):
\(3x-3+3\leq 2x\)
\(3x\leq 2x\)
Do obu stron nierówności dodajemy \(-2x\) (lub łatwiej powiedzieć: przenosimy \(2x\) na drugą stronę):
\(3x-2x\leq 0\)
\(x\leq 0\)
Otrzymaliśmy rozwiązanie, które najlepiej przedstawić w postaci przedziału liczbowego: \(\langle 0;+\infty)\).
Twierdzenie
Dla każdego dodatniego c prawdziwa jest równoważność: \(a>b \Leftrightarrow a \cdot c> b \cdot c\) oraz dla każdego ujemnego \(c\): \(a>b \Leftrightarrow a \cdot c<b\cdot c\).
Z powyższego twierdzenia wynika, że obie strony nierówności możemy pomnożyć (a więc i podzielić, czyli pomnożyć przez odwrotność tej liczby) przez dowolną liczbę różną od zera i otrzymamy wówczas równanie równoważne, pod warunkiem że przy mnożeniu obu stron nierówności przez liczbę ujemną zmieniamy znak mniejszości na znak większości i odwrotnie.
Aby śledzić tok rachunków, działanie takie zwykle zapisujemy za równaniem po ukośniku.
Przykłady
Rozwiązujemy nierówność:
\(-3x-1>5\) (przenosimy -1 na drugą stronę).
\(-3x>6 /:(-3)\) (dzielimy obie strony równania przez -3).
\(x<-2\)
Ponieważ dzieliliśmy obie strony nierówności przez liczbę ujemną, zmieniliśmy znak większości na znak mniejszości.
Pytania
Jak rozwiązywać nierówności?
Poniżej przedstawiamy linki do artykułów, w których pokazujemy, jak rozwiązujemy różne typy nierówności:
Powiązane materiały
© medianauka.pl, 2009-06-23, A-241
Data aktualizacji artykułu: 2023-05-01

 Równanie
Równanie Nierówność
Nierówność Rozwiązywanie równań
Rozwiązywanie równań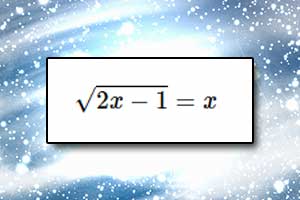 Metoda analizy starożytnych
Metoda analizy starożytnych Równania i nierówności — podstawy
Równania i nierówności — podstawy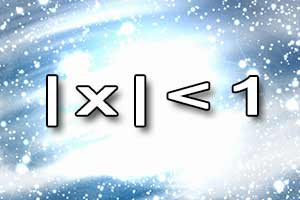 Nierówności z wartością bezwzględną
Nierówności z wartością bezwzględną