Nierówności trygonometryczne
Nierówność trygonometryczna jest to nierówność, w której niewiadoma występuje pod znakiem funkcji trygonometrycznej.
Przykłady
Przykłady nierówności trygonometrycznych:
- \(\sin{x}<\sqrt{2}\)
- \( tg(x-\frac{\pi}{2})\leq -1\)
- \(\sin{x}\geq\cos{x}\)
Rozwiązanie prostych nierówności najlepiej przeprowadzić w taki sposób, aby po jednej stronie nierówności znalazło się wyrażenie trygonometryczne elementarne (patrz równania trygonometryczne), a po drugiej wyrażenie liczbowe. Wówczas sporządzając odpowiedni wykres, można odczytać rozwiązanie wprost z wykresu.
Przykład
Rozwiążemy graficznie nierówność:
\(\sin{x}\geq \frac{1}{2}\)
Sporządzamy wykresy funkcji: \(y=\sin{x}, \ y=\frac{1}{2}\) i zaznaczamy wszystkie wartości funkcji sinus, które leżą powyżej lub na prostej \(y=\frac{1}{2}\).
Sporządzamy wykres:
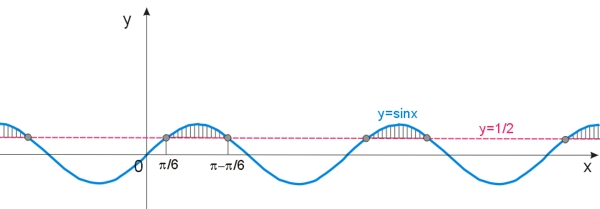
Zaznaczamy rozwiązania równania trygonometrycznego \(\sin{x}=\frac{1}{2}\), którego interpretacją geometryczną są punkty przecięcia obu wykresów. Jest to rozwiązanie równania elementarnego:
\(x=\frac{\pi}{6}+2k\pi \ \vee \ x=\pi-\frac{\pi}{6}+2k\pi, \ k\in C\)
\( x=\frac{\pi}{6}+2k\pi \ \vee \ x=\frac{5}{6}\pi+2k\pi, \ k\in C\)
Wszystkie wartości funkcji sinus większe lub równa \(\frac{1}{2}\) zawierają się w przedziale: \(\langle \frac{\pi}{6}+2k\pi;\frac{5}{6}\pi+2k\pi\rangle, \ k\in C\).
Rozwiązanie zaznaczono na rysunku poprzez zakreskowanie odpowiednich obszarów.
Zadania z rozwiązaniami

Zadanie nr 1.
Rozwiązać nierówność:
a) \(tgx\leq \sqrt{3}\)
b) \(2\cos{x}>4\)

Zadanie nr 2.
Rozwiązać nierówność:
a) \(\sin{(3x-\frac{\pi}{2})}<\sqrt{2}\)
b) \(ctg3x<1\)

Zadanie nr 3 — maturalne.
Rozwiąż nierówność \(\frac{2cos{x}-\sqrt{3}}{cos^2x}<0\) w przedziale \(\langle 0;2\pi\rangle\).
Powiązane materiały
© medianauka.pl, 2011-06-08, A-1363
Data aktualizacji artykułu: 2023-05-11

 Równania trygonometryczne
Równania trygonometryczne Rozwiązywanie równań trygonometrycznych
Rozwiązywanie równań trygonometrycznych Funkcje trygonometryczne sinus cosinus tangens
Funkcje trygonometryczne sinus cosinus tangens Sinus cosinus tangens cotangens 0 30 45 60 90 stopni
Sinus cosinus tangens cotangens 0 30 45 60 90 stopni Nauka wartości funkcji trygonometrycznych
Nauka wartości funkcji trygonometrycznych Wzory trygonometryczne, tożsamości trygonometryczne
Wzory trygonometryczne, tożsamości trygonometryczne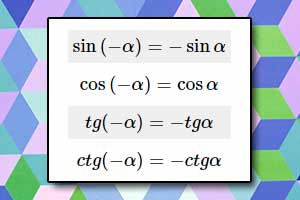 Wzory redukcyjne
Wzory redukcyjne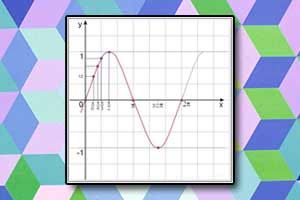 Wykres funkcji sinus
Wykres funkcji sinus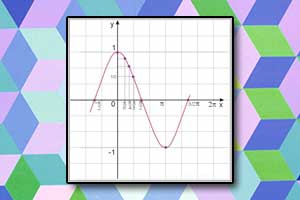 Wykres funkcji cosinus
Wykres funkcji cosinus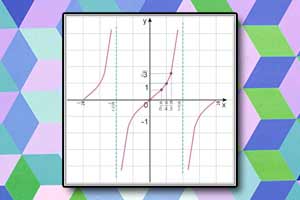 Wykres funkcji tangens
Wykres funkcji tangens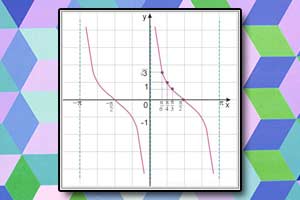 Wykres funkcji cotangens
Wykres funkcji cotangens