Wzory redukcyjne
Wzory redukcyjne z uwagi na ich wielość i różnorodność są trudne do zapamiętania, stąd oprócz przedstawienia samych wzorów proponujemy zapoznać się także ze sposobem, w jaki można sobie te wzory wyznaczyć samodzielnie za pomocą tak zwanego koła trygonometrycznego.
W poniższe tabeli zestawiono wzory redukcyjne dla funkcji trygonometrycznych.
Wzory redukcyjne dla kąta -α
| Dla kąta \(-\alpha\) |
| \(\sin{(-\alpha)}=-\sin{\alpha}\) |
| \(\cos{(-\alpha)}=\cos{\alpha}\) |
| \(tg{(-\alpha)}=-tg{\alpha}\) |
| \(ctg{(-\alpha)}=-ctg{\alpha}\) |
Zastosowanie koła trygonometrycznego do wyznaczenia powyższych zależności znajdziesz tutaj.
Wzory redukcyjne dla kąta 180°-α oraz 180°+α
| Dla kąta \(180°-\alpha\) | Dla kąta \(180°+\alpha\) |
| \(\sin{(180°-\alpha)}=\sin{\alpha}\) | \(\sin{(180°+\alpha)}=-\sin{\alpha}\) |
| \(\cos{(180°-\alpha)}=-\cos{\alpha}\) | \(\cos{(180°+\alpha)}=-\cos{\alpha}\) |
| \(tg{(180°-\alpha)}=-tg{\alpha}\) | \(tg{(180°+\alpha)}=tg{\alpha}\) |
| \(ctg{(180°-\alpha)}=-ctg{\alpha}\) | \(ctg{(180°+\alpha)}=ctg{\alpha}\) |
Zastosowanie koła trygonometrycznego do wyznaczenia powyższych zależności znajdziesz tutaj.
Wzory redukcyjne dla kąta 90°-α oraz 90°+α
| Dla kąta \(90°-\alpha\) | Dla kąta \(90°+\alpha\) |
| \(\sin{(90°-\alpha)}=\cos{\alpha}\) | \(\sin{(90°+\alpha)}=\cos{\alpha}\) |
| \(\cos{(90°-\alpha)}=\sin{\alpha}\) | \(\cos{(90°+\alpha)}=-\sin{\alpha}\) |
| \(tg{(90°-\alpha)}=ctg{\alpha}\) | \(tg{(90°+\alpha)}=-ctg{\alpha}\) |
| \(ctg{(90°-\alpha)}=tg{\alpha}\) | \(ctg{(90°+\alpha)}=-tg{\alpha}\) |
Zastosowanie koła trygonometrycznego do wyznaczenia powyższych zależności znajdziesz tutaj.
Wzory redukcyjne związane z okresem funkcji trygonometrycznej
| Dla dowolnej liczby całkowitej \(k\) |
| \(\sin{(\alpha+k\cdot 360°)}=\sin{\alpha}\) |
| \(\cos{(\alpha+k\cdot 360°)}=\cos{\alpha}\) |
| \(tg{(\alpha+k\cdot 180°)}=tg{\alpha}\) |
| \(ctg{(\alpha+k\cdot 180°)}=ctg{\alpha}\) |
Wzory redukcyjne dla kąta 45°-α oraz 45°+α
| Dla kąta \(45°-\alpha\) oraz \(45°+\alpha\) |
| \(\sin{(45°+\alpha)}=\cos{(45°-\alpha)}\) |
| \(\cos{(45°+\alpha)}=\sin{(45°-\alpha)}\) |
| \(tg{(45°+\alpha)}=ctg{(45°-\alpha)}\) |
| \(ctg{(45°+\alpha)}=tg{(45°-\alpha)}\) |
Koło trygonometryczne
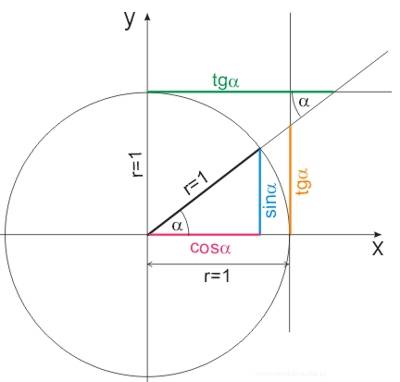
Powyższych wzorów nie trzeba uczyć się na pamięć, można je sobie dość łatwo wyprowadzić, korzystając z tak zwanego koła trygonometrycznego.
Jest to koło o środku w początku układu współrzędnych i promieniu \(r=1\). Można wówczas zaznaczyć pewne charakterystyczne odcinki, których długości są równe odpowiednim funkcjom trygonometrycznym kąta zgodnie z definicją. Koło takie zostało zilustrowane poniższym rysunkiem.
Dla przykładu zgodnie z definicją sinusa kąta jest on równy stosunkowi przyprostokątnej przeciwległej kątowi (odcinek zaznaczony kolorem niebieskim), do przeciwprostokątnej, a ponieważ przeciwprostokątna, to \(r=1\), więc długość odcinka zaznaczonego kolorem niebieskim jest równa sinusowi danego kąta.
W przypadku pozostałych funkcji trygonometrycznych jest podobnie, zawsze w mianowniku ułamka występuje liczba \(1\).
Jak wyznaczyć wzory redukcyjne dla kąta -α?
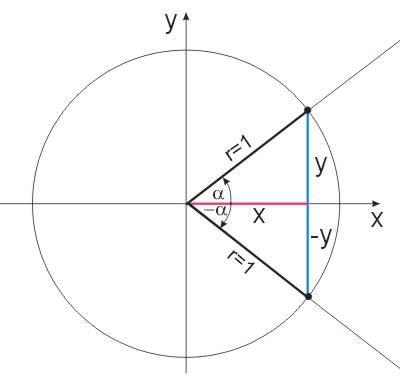
Rysujemy koło trygonometryczne i zaznaczamy odpowiednie kąty oraz współrzędne:
Mamy na podstawie rysunku:
\(\sin{\alpha}=\frac{y}{r}=\frac{y}{1}=y\)
oraz
\(\sin{(-\alpha)}=\frac{-y}{r}=\frac{-y}{1}=-y=-\sin{\alpha}\)
Natomiast dla funkcji cosinus:
\(\cos{\alpha}=\frac{x}{r}=\frac{x}{1}=x\)
oraz
\(\cos{(-\alpha)}=\frac{x}{r}=\frac{x}{1}=x=\cos{\alpha}\)
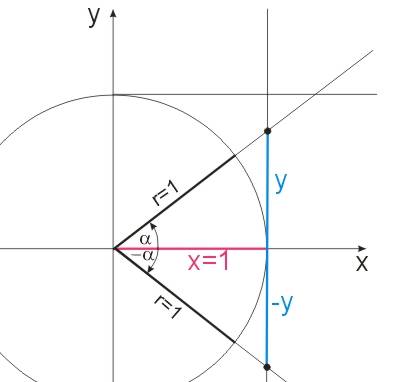
Dla funkcji tangens warto sporządzić osobny rysunek:
Mamy na podstawie rysunku:
\(tg{\alpha}=\frac{y}{x}=\frac{y}{1}=y\)
oraz
\(tg{(-\alpha)}=\frac{-y}{x}=\frac{-y}{1}=-y=-tg{\alpha}\)
Podobne wyprowadzenie wzoru redukcyjnego można przeprowadzić dla funkcji cotangens. Można także skorzystać bezpośrednio ze wzoru \(tg{\alpha}=\frac{1}{ctg{\alpha}}\) i od razu ustalić znak.
Dla pozostałych wzorów redukcyjnych postępujemy w identyczny sposób. Sporządzamy koło trygonometryczne, zaznaczamy kąt dany oraz kąt, dla którego określamy wzór redukcyjny, zaznaczamy odpowiednie odcinki i wyznaczamy kolejno funkcje trygonometryczne. Poniżej ograniczymy się tylko do niektórych funkcji trygonometrycznych.
Jak wyznaczyć wzory redukcyjne dla kąta 180°-α?
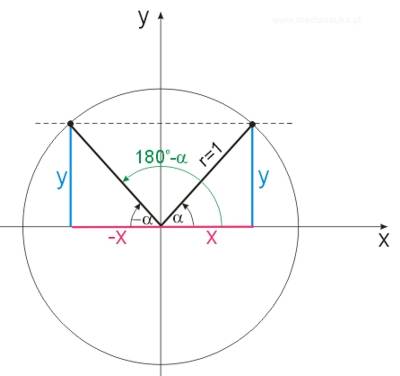
Rysujemy koło trygonometryczne i zaznaczamy odpowiednie kąty oraz współrzędne:
Mamy na podstawie rysunku:
\(\sin{\alpha}=\frac{y}{r}=\frac{y}{1}=y\)
oraz
\(\sin{(180°-\alpha)}=\frac{y}{r}=\frac{y}{1}=y=\sin{\alpha}\)
Natomiast dla funkcji cosinus:
\(cos{\alpha}=\frac{x}{r}=\frac{x}{1}=x\)
oraz
\(\cos{(180°-\alpha)}=\frac{-x}{r}=\frac{-x}{1}=-x=-\cos{\alpha}\)
Jak wyznaczyć wzory redukcyjne dla kąta 180°+α?
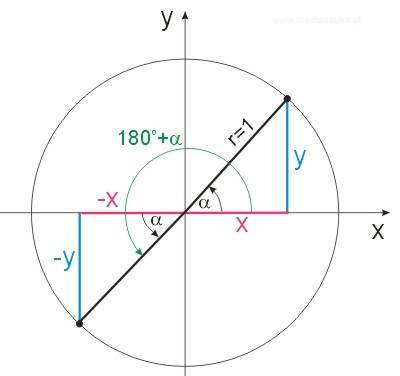
Rysujemy koło trygonometryczne i zaznaczamy odpowiednie kąty oraz współrzędne:
Mamy na podstawie rysunku:
\(\sin{\alpha}=\frac{y}{r}=\frac{y}{1}=y\)
oraz
\(\sin{(180°+\alpha)}=\frac{-y}{r}=\frac{-y}{1}=-y=-\sin{\alpha}\)
Natomiast dla funkcji cosinus:
\(\cos{\alpha}=\frac{x}{r}=\frac{x}{1}=x\)
oraz
\(\cos{(180°+\alpha)}=\frac{-x}{r}=\frac{-x}{1}=-x=-\cos{\alpha}\)
Jak wyznaczyć wzory redukcyjne dla kąta 90°-α?
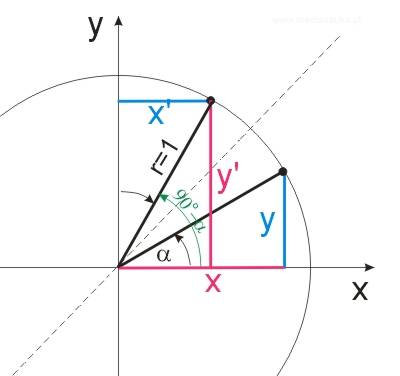
Rysujemy koło trygonometryczne i zaznaczamy odpowiednie kąty oraz współrzędne:
Ponieważ \(x=y', y=x'\) mamy na podstawie rysunku:
\(\sin{\alpha}=\frac{y}{r}=\frac{y}{1}=y\)
\(\cos{\alpha}=\frac{x}{r}=\frac{x}{1}=x\)
oraz
\(\sin{(90°-\alpha)}=\frac{y'}{r}=\frac{x}{r}=\cos{\alpha}\)
\(\cos{(90°-\alpha)}=\frac{x'}{r}=\frac{y}{r}=\sin{\alpha}\)
Jak wyznaczyć tangens takiego kąta? Wystarczy skorzystać ze wzoru:
\(tg{\alpha}=\frac{\sin{\alpha}}{\cos{\alpha}}\)
czyli:
\(tg{(90°-\alpha)}=\frac{\sin{(90°-\alpha)}}{\cos{(90°-\alpha)}}=\frac{\cos{\alpha}}{\sin{\alpha}}=ctg{\alpha}\)
Przykłady zastosowania wzorów redukcyjnych
Wzory redukcyjne wykorzystujemy przy obliczaniu wartości funkcji trygonometrycznych innych kątów niż 0°, 30°, 45°, 60°, 90°. Oto kilka przykładów.
Przykład 1
Obliczyć \(\sin{405°}\).
Rozwiązanie: Korzystamy ze wzoru redukcyjnego dla pełnego kąta:
\(\sin{405°}=\sin{(360°+45°)}=\sin{45°}= \frac{\sqrt{2}}{2}\)
Przykład 2
Obliczyć \(tg{(-60°)}\).
Rozwiązanie: Korzystamy ze wzoru redukcyjnego dla kąta \(-\alpha\):
\(tg{(-60°)}=-tg{60°}=-\sqrt{3}\)
Przykład 3
Obliczyć \(\sin{225°}\).
Rozwiązanie: Korzystamy ze wzoru redukcyjnego dla kąta \(180°+\alpha\):
\(\sin{225°}=\sin{(180°+45°)}=-\sin{45°}=-\frac{\sqrt{2}}{2}\)
Pytania
Czy jest możliwa zamiana sinusa na cosinus?
Do tego między innymi służą wzory trygonometryczne redukcyjne. Zobacz wzory redukcyjne dla kąta \(90°-alpha\) oraz \(90°+\alpha\).
Zadania z rozwiązaniami
Zadanie nr 1.
Obliczyć:
a) \(\sin{30°}\)
b) \(\cos{3285°}\)
c) \(tg{1125°}\)
d) \(ctg{210°}\)
Zadanie nr 2.
Obliczyć:
a) \(\sin{(-45°)}\)
b) \(ctg{(-60°)}\)
c) \(\cos{(-90°)}\)
Zadanie nr 3.
Obliczyć:
a) \(\sin{120°}\)
b) \(\cos{135°}\)
c) \(\cos{240°}\)
d) \(\sin{225°}\)
Zadanie nr 5.
Obliczyć:
a) \(\sin{960°}\)
b) \(tg{2115°}\)
c) \(\cos{2760°}\)
Zadanie nr 6.
Sprowadzić do prostszej postaci:
a) \(\sin{(180^o-x)}+\cos{(90^o+x)}\)
b) \(\cos{(\pi-x)}\sin{(\frac{\pi}{2}-x)}\)
c) \(tg{(270^o-x)}tg{(180^o+x)}\)
Zadanie nr 7.
Sprowadzić do prostszej postaci:
a) \(\sin{(-x)}-\cos{(270°-x)}\)
b) \(\sin{(x-90°)}\)
c) \(\cos{(x-\pi)}\)
Zadanie nr 8 — maturalne.
Jeśli \(m=\sin{50°}\), to
A. \(m=\sin40°\)
B. \(m=\cos40°\)
C. \(m=\cos50°\)
D. \(m=tg50°\)
Zadanie nr 9 — maturalne.
Liczba \(cos{12°}\cdot \sin{78°}+\sin{12°}\cdot \cos{78°}\) jest równa
A. \(\frac{1}{2}\)
B. \(\frac{\sqrt{2}}{2}\)
C. \(\frac{2}{9}\)
D. 1
Powiązane materiały
Sinus cosinus tangens cotangens 0 30 45 60 90 stopni
Nauka wartości funkcji trygonometrycznych
Funkcje trygonometryczne sinus cosinus tangens
Wykres funkcji sinus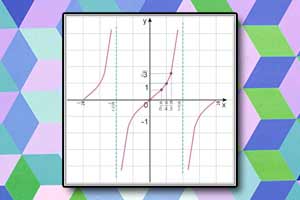
Wykres funkcji tangens
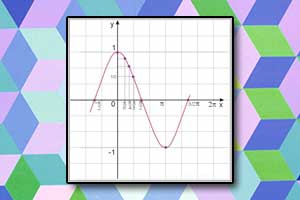Wykres funkcji cosinus
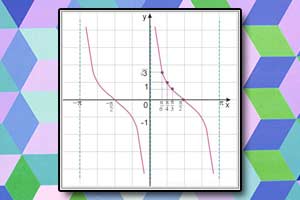Wykres funkcji cotangens
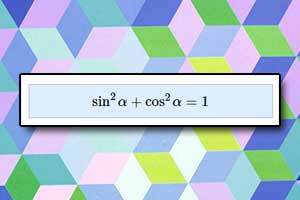Wzory trygonometryczne, tożsamości trygonometryczne
Twierdzenie sinusów, cosinusów i tangensów
Funkcje cyklometryczne© medianauka.pl, 2011-04-06, A-1285
Data aktualizacji artykułu: 2023-07-22