Funkcje cyklometryczne

Funkcje cyklometryczne (funkcje kołowe) są to funkcje odwrotne do funkcji trygonometrycznych zmiennej rzeczywistej. Oznaczamy je i czytamy odpowiednio:

arcsin — arcus sinus

arccos — arcus cosinus

arctg — arcus tangens

arcctg — arcus cotangens

Aby istniała funkcja cyklometryczna danej funkcji, funkcja ta musi być rosnąca lub malejąca. Funkcje trygonometryczne nie spełniają tego warunku w całej swej dziedzinie, dlatego zawężamy je do przedziałów, w których warunek ten jest spełniony.

W kolejnych artykułach omawiamy poszczególne funkcje kołowe, prezentujemy wykresy funkcji cyklometrycznych i omawiamy własności tych funkcji.

Powiązane materiały

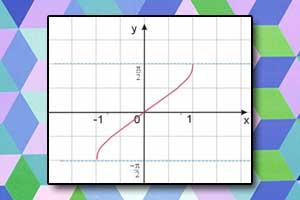Funkcja arcus sinus arcsin

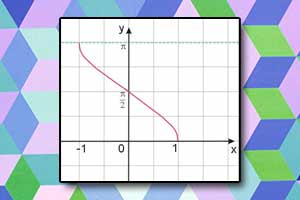Funkcja arcus cosinus arccos

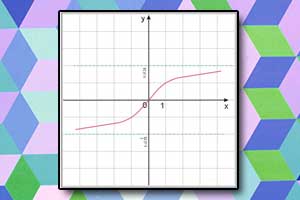Funkcja arcus tangens arctg

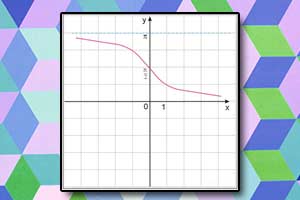Funkcja arcus cotangens arcctg