Arcus cosinus — arccos

Arcus cosinus jest funkcją odwrotną do funkcji $y = \cos x$ określonej w przedziale $[0, π]$ . Funkcję tę oznaczamy następująco: $y = a r c c o s x$ , a zapis ten oznacza, że $x = \cos y$ i $y \in [0, π]$ .

Przykład

Obliczyć $a r c c o s 1$ .

Aby wyznaczyć wskazaną wartość funkcji arcus cosinus, wystarczy skorzystać z definicji i obliczyć równanie: $\cos y = 1$ . Jest to równanie trygonometryczne elementarne, które ma nieskończenie wiele rozwiązań ( $y = 2 k π, k \in Z$ ), my jednak musimy się ograniczyć do przedziału $[0, π]$ , mamy więc jedno rozwiązanie: $a r c c o s 1 = 0$ .

Wykres funkcji arccos

Aby wyznaczyć wykres funkcji $y = a r c c o s x$ , postępujemy zgodnie z definicją:

W układzie współrzędnych, gdzie oś $y$ jest osią poziomą, a oś $x$ osią pionową sporządzamy wykres funkcji $x = \cos y$ , ale jedynie w przedziale $[0, π]$ .
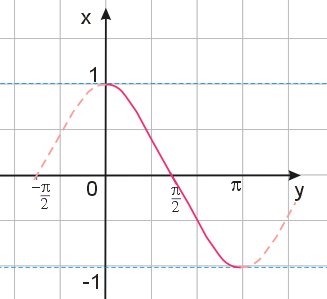
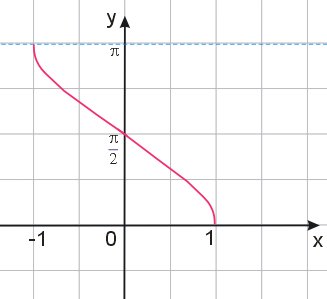
Po odpowiednim obrocie w przestrzeni i otrzymujemy wykres funkcji $y = a r c c o s x$ w typowym układzie współrzędnych.

Powiązane materiały

Funkcje cyklometryczne

Funkcja arcus sinus arcsin

Funkcja arcus tangens arctg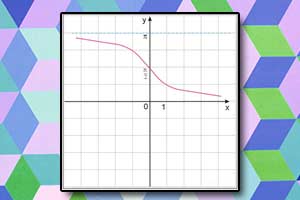

Funkcja arcus cotangens arcctg