Równania trygonometryczne

Definicja

Równanie trygonometryczne jest to równanie, w którym niewiadome występują wyłącznie pod znakami funkcji trygonometrycznych.

Przykład

Oto przykłady równań trygonometrycznych:

$\sin(x-2)=1\\ \frac{1}{\sin{x}}-3=\cos{x}\\ tg{4x}=0$

Rozwiązania równań trygonometrycznych

Rozwiązaniem równania trygonometrycznego możne być kąt skierowany lub w innej interpretacji miara kąta skierowanego. Mówimy więc o dwóch interpretacjach rozwiązania równania trygonometrycznego i dwóch nowych pojęciach:

Rozwiązanie podstawowe równania trygonometrycznego jest to zbiór wszystkich kątów skierowanych spełniających dane równanie.

Rozwiązanie ogólne równania trygonometrycznego jest to zbiór wszystkich miar kątów skierowanych spełniających dane równanie.

Przykład

Rozwiążemy równanie trygonometryczne $\sin{x}=a$ .

Sporządzamy koło trygonometryczne:

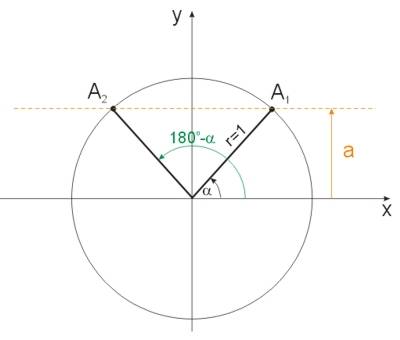
Jeżeli a jest liczbą mniejszą od 1 i większą od -1 (czyli |a|<1), to odpowiednia prosta (zaznaczona liczbą przerywaną na rysunku) przecina koło trygonometryczne w dwóch punktach: A₁, A₂, wyznaczając dwa kąty, które spełniają równanie. Kąty te można wyrazić za pomocą miary głównej. Otrzymujemy więc rozwiązanie podstawowe: $x_1=\alpha \, \ x_2=180^o-\alpha$ .

Wszystkie miary stopniowe danego kąta otrzymamy, jeśli do miary tego kąta dodamy dowolną całkowitą wielokrotność miary kąta pełnego. Mamy więc rozwiązanie ogólne: $x_1=\alpha +k\cdot 360^o \, \ x_2=180^o-\alpha+k\cdot 360^o, k\in C$ .

Jeżeli a>1 lub a< -1, czyli |a|>1 to równanie to nie ma rozwiązań. (odpowiednia prosta nie przecina koła trygonometrycznego (patrz rysunek).

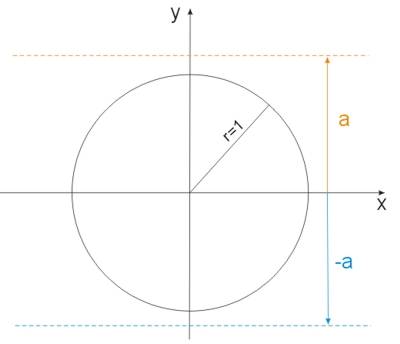
Jeżeli a=1, to:

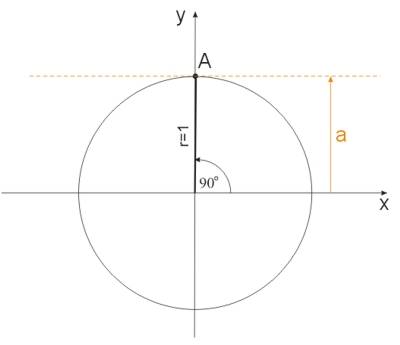
mamy wówczas jedno rozwiązanie podstawowe i rozwiązanie ogólne: $x=90^o+k\cdot 360^o,\ k\in C$ .

Jeżeli a=-1, to:

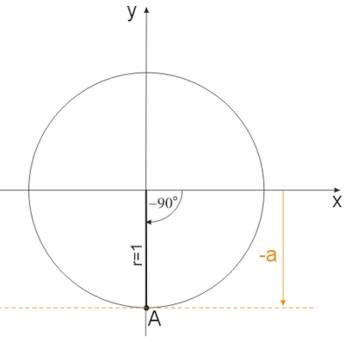
mamy wówczas jedno rozwiązanie podstawowe i rozwiązanie ogólne: $x=-90^o+k\cdot 360^o,\ k\in C$ .

Reasumując:

Przypadek	Rozwiązanie podstawowe	Rozwiązanie ogólne
\|a\|>1	brak rozwiązań	brak rozwiązań
a=1		$x=90^o+k\cdot 360^o,\ k\in C$
a=-1		$x=-90^o+k\cdot 360^o,\ k\in C$
\|a\|<1	$x=\alpha\ \vee \ x=180^o-\alpha$	$x=\alpha+k\cdot 360^o\ \vee \ x=180^o-\alpha+k\cdot 360^o,\ k\in C$

Wzory trygonometryczne a równania trygonometryczne

Przy rozwiązywaniu równań trygonometrycznych bardzo często przydają się wzory trygonometryczne. Warto się z nimi zapoznać. Wzory trygonometryczne przedstawiamy i omawiamy tutaj.

Równania elementarne

Równania:
$\sin{x}=a,\ \cos{x}=a,\ tgx=a,\ ctgx=a$
nazywamy równaniami elementarnymi.

Rozwiązując równania trygonometryczne staramy się doprowadzić je do równania elementarnego. Powyżej pokazano sposób rozwiązania jednego z takich równań. W praktyce należy pamiętać rozwiązania równań elementarnych.

Poniżej zostały przedstawione rozwiązania wszystkich równań elementarnych:

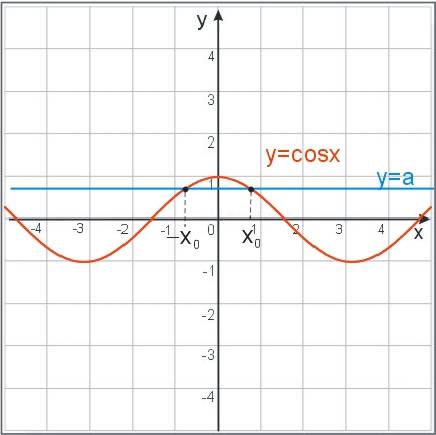
$(\sin{x}=a \ \wedge \ |a|\leq 1) \Leftrightarrow x=x_0+2k\pi \ \vee \ x=(\pi-x_0)+2k\pi,\ k\in C$
$(\cos{x}=a \ \wedge \ |a|\leq 1) \Leftrightarrow x=x_0+2k\pi \ \vee \ x=-x_0+2k\pi,\ k\in C$
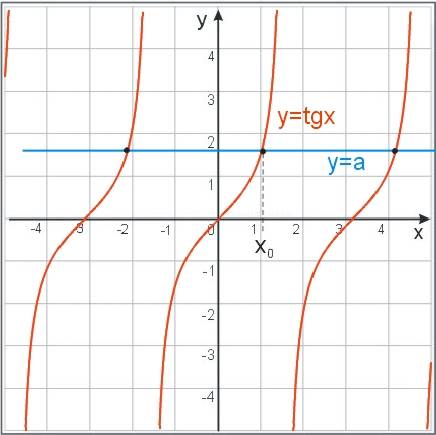
$tgx=a \Leftrightarrow x=x_0+k\pi,\ k\in C$
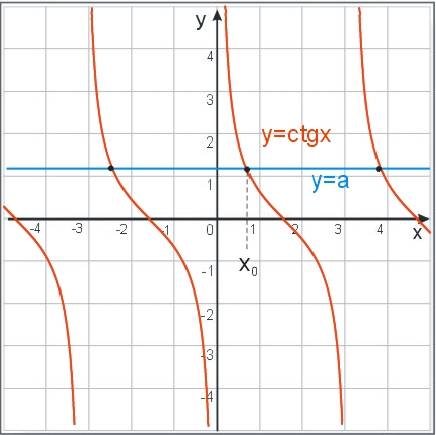
$ctgx=a \Leftrightarrow x=x_0+k\pi, ,\ k\in C$

x₀ - najmniejsze dodatnie rozwiązanie
Gdy |a|>1, równania sinx=a, cosx=a nie mają rozwiązania.

Rozwiązania powyższe dobrze widać na wykresie:

Pytania

Jak rozwiązać równania trygonometryczne?

Na to pytanie odpowiadamy w kolejnym artykule: Rozwiązywanie równań trygonometrycznych.

Ile rozwiązań ma równanie trygonometryczne?

O ile równanie trygonometryczne posiada rozwiązanie, to często tych rozwiązań jest nieskończenie wiele, z uwagi na to, że funkcja trygonometryczna to funkcja okresowa.

Zadania z rozwiązaniami

Zadania związane z tematem:
Równania trygonometryczne

Zadanie - równanie trygonometryczne
Rozwiązać równanie:
a)
b) $\sqrt{2}\sin{2x}=1$

Pokaż rozwiązanie zadania

Zadanie - równanie trygonometryczne
Rozwiązać równanie:
a) $ctg3x=\sqrt{3}$
b) $2\cos{3x}=\sqrt{2}$
c) $\cos{5x}=\sqrt{2}$

Pokaż rozwiązanie zadania

Zadanie maturalne nr 4, matura 2015 (poziom rozszerzony)
Równanie 2sinx+3cosx=6 w przedziale (0,2π)

A. nie ma rozwiązań rzeczywistych.
B. ma dokładnie jedno rozwiązanie rzeczywiste.
C. ma dokładnie dwa rozwiązania rzeczywiste.
D. ma więcej niż dwa rozwiązania rzeczywiste.

Pokaż rozwiązanie zadania

Zadanie maturalne nr 7, matura 2018 (poziom rozszerzony)

Rozwiąż równanie 2cos²x+3sinx=0 w przedziale < -π/2; 3π/2>.

Pokaż rozwiązanie zadania

Inne zagadnienia z tej lekcji

Funkcje trygonometryczne sinus cosinus tangens

Definicja funkcji trygonometrycznych kąta ostrego: sinus, cosinus, tangens, cotangens, secans, cosecans.

Sinus cosinus tangens cotangens 0 30 45 60 90 stopni

Poniższa tabela przedstawia wartości funkcji trygonometrycznych dla często używanych miar kątów.

Nauka wartości funkcji trygonometrycznych

Nauka wartości podstawowych funkcji trygonometrycznych on-line za pomocą darmowej aplikacji

Wykres funkcji sinus

Wykresem funkcji sinus jest krzywa, którą nazywamy sinusoidą.

Wykres funkcji cosinus

Wykresem funkcji cosinus jest cosinusoida.

Wykres funkcji tangens

Wykresem funkcji tangens jest tangensoida.

Wykres funkcji cotangens

Wykresem funkcji cotangens jest cotangensoida.

Wzory trygonometryczne, tożsamości trygonometryczne

Podstawowe wzory trygonometryczne (tożsamości trygonometryczne) oraz przykłady ich stosowania.

Wzory redukcyjne

Wzory redukcyjne z omówieniem sposobu ich wyznaczania za pomocą koła trygonometrycznego.

Rozwiązywanie równań trygonometrycznych

Rozwiązywanie równań trygonometrycznych metodą podstawiania, z wykorzystaniem tożsamości trygonometrycznych, metody równań równoważnych i analizy starożytnych

Nierówności trygonometryczne

Nierówność trygonometryczna jest to nierówność, w której niewiadoma występuje pod znakiem funkcji trygonometrycznej.