Rozwiązywanie równań trygonometrycznych
Jak rozwiązywać równania trygonometryczne? Poznamy tu dwie metody. Rozwiązywanie równań trygonometrycznych elementarnych omówiliśmy w poprzednim artykule (link na końcu artykułu).
Metoda podstawiania
Jedną z metod rozwiązywanie równań trygonometrycznych jest metoda podstawiania. W równaniu trygonometrycznym można zastosować zmienną pomocniczą, w wyniku czego otrzymujemy zwykle zwykłe równanie algebraiczne, po którego rozwiązaniu otrzymujemy pierwiastki, które przy zastosowaniu pierwotnej zmiennej, prowadzą do równań trygonometrycznych elementarnych.
Przykład
Rozwiążemy równanie \(2\cos^2{x}-3\cos{x}+1=0\).
Zastosujemy podstawienie \(\cos{x}=t\) i otrzymujemy: \(2t^2-3t+1=0\), czyli równanie kwadratowe. Rozwiązujemy je.
\(\Delta=1\)
\( t_1=\frac{3-1}{4}=\frac{1}{2}\)
\(t_2=\frac{3+1}{4}=1\)
Wracamy do zmiennej \(x\):
\(\cos{x}=1 \vee \cos{x}=\frac{1}{2}\)
Mamy rozwiązanie podstawowe \(0, \frac{\pi}{3}, -\frac{\pi}{3}\).
Możemy zapisać rozwiązanie ogólne obu równań:
\(x_1=2k\pi \ \vee \ x_2=\frac{\pi}{3}+2k\pi \ \vee \ x_3=-\frac{\pi}{3}+2k\pi, \ k\in C\)
Korzystanie z tożsamości trygonometrycznych
Przy rozwiązywaniu równań trygonometrycznych staramy się korzystać z tożsamości trygonometrycznych tak, aby doprowadzić równanie do postaci równania elementarnego lub takiego, dla którego można zastosować inne metody rozwiązywania równań. Oto prosty przykład:
Przykład
Rozwiążemy równanie:
\(\frac{\sin{x}-\cos{x}}{\cos{x}}=0\)
Przekształcamy równanie:
\(\frac{\sin{x}-\cos{x}}{\cos{x}}=0\)
\( \frac{\sin{x}}{\cos{x}}-\frac{\cos{x}}{\cos{x}}=0\)
\( \frac{\sin{x}}{\cos{x}}-1=0\)
Stosujemy tożsamość trygonometryczną:
\(tgx=\frac{\sin{x}}{\cos{x}}\)
Otrzymujemy:
\(tgx-1=0\)
\(tgx=1\)
Rozwiązanie podstawowe to \(\frac{\pi}{4}\), rozwiązanie ogólne: \(x=\frac{\pi}{4}+k\pi,\ k\in C\).
Metoda równań równoważnych i analizy starożytnych
Metoda analizy starożytnych została omówiona tutaj. Zastosujemy je na poniższym przykładzie:
Przykład 1
Rozwiążemy równanie \(\sin{x}-\cos{x}=-1\).
Przekształcimy je do postaci:
\(\sin{x}+1=\cos{x}/^2\)
\(\sin^2{x}+2\sin{x}+1=\cos^2{x}\)
Korzystamy z jedynki trygonometrycznej:
\(\sin^2{x}+2\sin{x}+1=1-\sin^2{x}\)
\(2\sin^2{x}+2\sin{x}=0/:2\)
\( \sin{x}(\sin{x}+1)=0\)
Iloczyn dwóch liczb jest zerem, gdy jedna z nich jest zerem lub obie są równe zeru, więc:
\(\sin{x}=0 \ \vee \ \sin{x}+1=0\)
\(\sin{x}=0 \ \vee \ \sin{x}=-1\)
Otrzymujemy rozwiązanie podstawowe:
\(x=0\) lub \( x=\pi\) lub \( x=\frac{3}{2}\pi\)
Dokonujemy sprawdzenia równania \(\sin{x}-\cos{x}=-1\):
- Dla \(x=0\): \(\sin{0}-\cos{0}=-1 \ \Leftrightarrow 0-1=-1\) — zdanie prawdziwe.
- Dla \(x=\pi\): \(\sin{\pi}-\cos{\pi}=-1 \ \Leftrightarrow 0+1=-1\) — zdanie nieprawdziwe.
- Dla \(x=\frac{3}{2}\pi\): \(\sin{\frac{3}{2}\pi}-\cos{\frac{3}{2}\pi}=-1 \ \Leftrightarrow -1-0=-1\) — zdanie prawdziwe.
Piszemy rozwiązanie ogólne: \(x=2k\pi\) lub \(x=\frac{3}{2}\pi+2k\pi, k\in C\).
Przykład 2
Rozwiążemy równanie \(ctg4x=1\).
Mamy:
\(4x=\frac{\pi}{4}+k\pi/:4\ , \ k\in C\)
\(x=\frac{\pi}{16}+k\frac{\pi}{4}\)
Zadania z rozwiązaniami

Zadanie nr 7.
Rozwiązać równanie: \(\cos{(2x-\frac{\pi}{4})}=-\frac{\sqrt{2}}{2}\).

Zadanie nr 10 — maturalne.
Równanie \(2sinx+3cosx=6\) w przedziale \((0,2\pi)\)
A. nie ma rozwiązań rzeczywistych.
B. ma dokładnie jedno rozwiązanie rzeczywiste.
C. ma dokładnie dwa rozwiązania rzeczywiste.
D. ma więcej niż dwa rozwiązania rzeczywiste.

Zadanie nr 11 — maturalne.
Rozwiąż równanie \(\cos{2x}=\sin{x}+1\) w przedziale \(\langle 0,2\pi \rangle\).

Zadanie nr 12 — maturalne.
Rozwiąż równanie \(3\cos{2x}+10 \cos^2{x}=24\sin{x}−3\) dla \(x\in \langle 0, 2\pi\rangle\).

Zadanie nr 13 — maturalne.
Rozwiąż równanie \(\cos{2x}=\frac{\sqrt{2}}{2}(\cos{x}-\sin{x})\) w przedziale \(\langle 0; \pi \rangle\).

Zadanie nr 14 — maturalne.
Rozwiąż równanie \(4\sin{(4x)}\cos{(6x)}=2\sin{(10x)}+1\). Zapisz obliczenia.
Powiązane materiały
© medianauka.pl, 2011-05-31, A-1339
Data aktualizacji artykułu: 2023-05-09

 Równania trygonometryczne
Równania trygonometryczne Nierówności trygonometryczne
Nierówności trygonometryczne Funkcje trygonometryczne sinus cosinus tangens
Funkcje trygonometryczne sinus cosinus tangens Sinus cosinus tangens cotangens 0 30 45 60 90 stopni
Sinus cosinus tangens cotangens 0 30 45 60 90 stopni Nauka wartości funkcji trygonometrycznych
Nauka wartości funkcji trygonometrycznych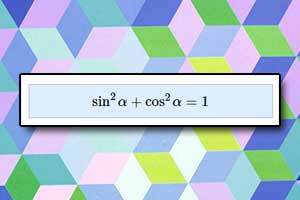 Wzory trygonometryczne, tożsamości trygonometryczne
Wzory trygonometryczne, tożsamości trygonometryczne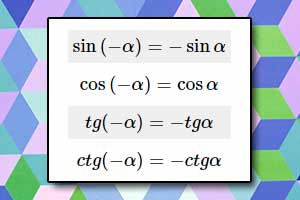 Wzory redukcyjne
Wzory redukcyjne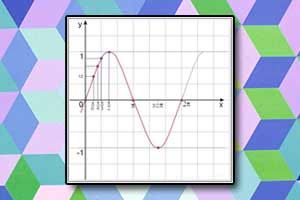 Wykres funkcji sinus
Wykres funkcji sinus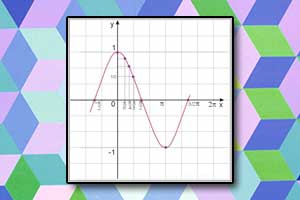 Wykres funkcji cosinus
Wykres funkcji cosinus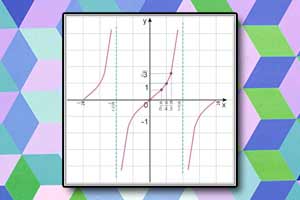 Wykres funkcji tangens
Wykres funkcji tangens Wykres funkcji cotangens
Wykres funkcji cotangens