Wzory trygonometryczne
W niniejszym artykule przedstawiamy podstawowe wzory trygonometryczne, o których często mówimy także tożsamości trygonometryczne.
Między funkcjami trygonometrycznymi kąta \(\alpha\) zachodzą następujące związki (tożsamości trygonometryczne):
Jedynka trygonometryczna
Dowód
Na podstawie twierdzenia Pitagorasa mamy:
\(a^2+b^2=c^2/:c^2\)
\( \frac{a^2}{c^2} + \frac{b^2}{c^2}=1\)
(\(\frac{a}{c})^2+(\frac{b}{c})^2=1\)
\( \sin^2{\alpha}+ \cos^2{\alpha}=1\)
Jedynka trygonometryczna to jeden z najczęściej występujący wzorów w zadaniach z trygonometrii. Obok przedstawiamy dowód tej tożsamości trygonometrycznej.
Powyższy wzór nosi też inne nazwy:
- wzór jednostkowy
- jedność trygonometryczna
- trygonometryczne twierdzenie Pitagorasa
Oto inne, bardzo często wykorzystywane w kursie matematyki wzory:
Sinus, cosinus, tangens i cotangens sumy kątów
Oto wzory na sinus sumy kątów, cosinus sumy kątów, tangens i cotangens sumy kątów:
\(\sin({\alpha+\beta})= \sin{\alpha}\cos{\beta} + \cos{\alpha}\sin{\beta}\)
\( \cos({\alpha+\beta}) = \cos{\alpha}\cos{\beta}-\sin{\alpha}\sin{\beta}\)
\( tg({\alpha+\beta}) = \frac{tg{\alpha}+tg{\beta}}{1-tg{\alpha}tg{\beta}}\)
\( ctg({\alpha+\beta}) = \frac{ctg{\alpha}ctg{\beta}-1}{ctg{\alpha}+ctg{\beta}}\)
Sinus, cosinus, tangens i cotangens kątów
Oto wzory na sinus różnicy kątów, cosinus różnicy kątów, tangens i cotangens różnicy kątów:
\(\sin({\alpha-\beta})= \sin{\alpha}\cos{\beta}-\cos{\alpha}\sin{\beta}\)
\(\cos({\alpha-\beta}) =\cos{\alpha}\cos{\beta} + \sin{\alpha}\sin{\beta}\)
\( tg({\alpha-\beta})=\frac{tg{\alpha}-tg{\beta}}{1+tg{\alpha}tg{\beta}}\)
\(ctg({\alpha-\beta}) = \frac{ctg{\alpha}ctg{\beta} +1}{ctg{\alpha}-ctg{\beta}}\)
Funkcje trygonometryczne podwojonego kąta
Wzory na sinus podwojonego kąta, cosinus podwojonego kąta i tangens podwojonego kąta:
\(\sin{2\alpha}=2\sin{\alpha}\cdot \cos{\alpha}\)
\(\cos{2\alpha}=\cos^2{\alpha}-\sin^2{\alpha}\)
\(tg{2\alpha}=\frac{2tg{\alpha}}{1-tg^2{\alpha}}\)
Funkcje potrojonego kąta
Wzory na sinus potrojonego kąta, cosinus potrojonego kąta:
\(\sin{3\alpha}=3\sin{\alpha}-4\sin^3{\alpha}\)
\(\cos{3\alpha}=4\cos^3{\alpha}-3\cos{\alpha}\)
Funkcje trygonometryczne połowy kąta — wzory połówkowe
Oto wzory połówkowe:
\(\sin{\frac{\alpha}{2}}=\pm\sqrt{\frac{1-\cos{\alpha}}{2}}\)
\( \cos{\frac{\alpha}{2}} =\pm\sqrt{\frac{1+\cos{\alpha}}{2}}\)
\( tg{\frac{\alpha}{2}}=\pm\sqrt{\frac{1-\cos{\alpha}}{1+\cos{\alpha}}}\)
\(tg{\frac{\alpha}{2}}=\frac{1-\cos{\alpha}}{\sin{\alpha}} =\frac{\sin{\alpha}}{1+\cos{\alpha}}\)
Sumy i różnice funkcji trygonometrycznych
Wzory na sumę sinusów, sumę cosinusów oraz różnicy sinusów i cosinusów są następujące:
\(\sin{\alpha}+\sin{\beta}= 2\sin\frac{\alpha+\beta}{2}\cos{\frac{\alpha-\beta}{2}}\)
\(\sin{\alpha}-\sin{\beta}= 2\cos\frac{\alpha+\beta}{2}\sin{\frac{\alpha-\beta}{2}}\)
\( \cos{\alpha}+\cos{\beta}= 2\cos\frac{\alpha+\beta}{2}\cos{\frac{\alpha-\beta}{2}}\)
\(\cos{\alpha}-\cos{\beta}=-2\sin\frac{\alpha+\beta}{2}\sin{\frac{\alpha-\beta}{2}}\)
A oto kilka przykładów zastosowania powyższych wzorów trygonometrycznych:
Przykład 1
Wiadomo, że \(\sin{\alpha}=0,3\). Obliczyć \(\cos{\alpha}, tg{\alpha}, ctg{\alpha}\).
Wyznaczamy cosinus kąta, korzystając z jedynki trygonometrycznej:
\(\sin^2{\alpha}+\cos^2{\alpha}=1\)
\(\cos^2{\alpha}=1-\sin^2{\alpha}\)
\(\cos{\alpha}=\pm\sqrt{1-\sin^2{\alpha}}\)
\(\cos{\alpha}=\pm\sqrt{1-0,3^2}=\pm\sqrt{1-0,09}=\)
\(=\pm\sqrt{0,91}\approx\pm0,954\)
Wyznaczamy tangens kąta:
\(tg{\alpha}=\frac{\sin{\alpha}}{\cos{\alpha}}\approx\frac{0,3}{\pm0,954}\approx\pm 0,3145\)
Wyznaczamy cotangens kąta:
\(ctg{\alpha}=\frac{1}{tg{\alpha}}\approx\frac{1}{\pm0,3145}\approx \pm 3,1797\)
Przykład 2
Obliczyć \(\sin{75°}\).
Skorzystamy ze wzoru na sinus sumy kątów:
\(\sin{75°}=\sin{(45°+30°)}=\sin{45^0}\cos{30°}+\cos{45°}\sin{30°}=\\ =\)
\(=\frac{\sqrt{2}}{2}\cdot \frac{\sqrt{3}}{2}+\frac{\sqrt{2}}{2}\cdot \frac{1}{2}=\)
\(=\frac{\sqrt{6}+\sqrt{2}}{4}\)
Przykład 3
Obliczyć \(\cos{120°}\)
Korzystamy ze wzoru na cosinus podwojonego kąta:
\(\cos{120°}=\cos{(2\cdot 60°)}=\cos^2{60°}-\sin^2{60°}=\)
\(=(\frac{1}{2})^2-(\frac{\sqrt{3}}{2})^2=\)
\(=\frac{1}{4}-\frac{3}{4}=-\frac{2}{4}=-\frac{1}{2}\)
Przykład 4
Obliczyć \(\sin{120°}+\sin{60°}\)
Korzystamy ze wzoru na sumę sinusów kąta:
\(\sin{120°}+\sin{60°}=\)
\(=2\sin{\frac{120°+60°}{2}}\cos{\frac{120°-60°}{2}}=\)
\(=2\sin{90°}\cos{30°}=2\cdot 1\cdot \frac{1}{2}=1\)
Pozostałe wzory
To nie jedyne wzory trygonometryczne. W osobnych artykułach omawiamy:
Zadania z rozwiązaniami

Zadanie nr 3.
Wiedząc, że \(\sin{x}=0,2\) oblicz \(\cos{2x}, \sin{2x}, tg{2x}\).

Zadanie nr 4.
Obliczyć
a) \(\sin{75°}+\sin{15°}\)
b) \(\cos{75°}+\cos{15°}\)
c) \(\sin{75°}-\sin{15°}\)
d) \(\cos{75°}-\cos{15°}\)

Zadanie nr 5.
Udowodnić tożsamość:
a) \(tg{\alpha}+ctg{\alpha}=\frac{1}{\sin{\alpha}\cos{\alpha}}\)
b) \(tg{\alpha}-tg{\beta}=\frac{\sin{(\alpha-\beta)}}{\cos{\alpha}\cos{\beta}}\)
c) \(\sin^4{\alpha}-cos^4{\alpha}=2\sin^2{\alpha}-1\)

Zadanie nr 6.
Udowodnić tożsamość:
a) \(tg{\alpha}\sin{2\alpha}=2\sin^2{\alpha}\)
b) \(\frac{1}{1-\sin{x}}+\frac{1}{1+\sin{x}}=\frac{2}{\cos^2{x}}\)
c) \(\frac{\sin{5x}+\sin{3x}}{\cos{5x}+\cos{3x}}=tg{4x}\)

Zadanie nr 7.
Udowodnić tożsamość: \(tg(45^o-\frac{x}{2})+tg{x}=\frac{1}{\cos{x}}\).

Zadanie nr 8.
Udowodnić tożsamość:
a) \(\frac{\sin{x}}{1+\cos{x}}=\frac{1-\cos{x}}{\sin{x}}\)
b) \(tg(45^o+x)tg(45^o-x)=1\)
c) \(\cos{x}+\sin{x}=\sqrt{2}\sin(45^o+x)\)
d) \(tg{x}+ctg{x}=\frac{2}{\sin{2x}}\)
e) \(\frac{1+tg{x}}{1-tg{x}}=tg(45^o+x)\)

Zadanie nr 9 — maturalne.
Dla każdego kąta ostrego α iloczyn \(\frac{cos\alpha}{1-\sin^2\alpha}\cdot \frac{1-cos^2\alpha}{sin\alpha}\) jest równy
A. \(\sin{\alpha}\)
B. \(tg\alpha\)
C. \(\cos{\alpha}\)
D. \(\sin^2{\alpha}\)

Zadanie nr 10 — maturalne.
Jeżeli \(0°<\alpha <90°\) oraz \(tg\alpha=2\sin{\alpha}\), to:
A. \(\cos{\alpha}=\frac{1}{2}\)
B. \(\cos{\alpha}=\frac{\sqrt{2}}{2}\)
C. \(\cos{\alpha}=\frac{\sqrt{3}}{2}\)
D. \(\cos{\alpha}=1\)

Zadanie nr 11 — maturalne.
Jeżeli \(\alpha\) jest kątem ostrym oraz \(tg\alpha=\frac{2}{5}\), to wartość wyrażenia \(\frac{3\cos{\alpha}-2\sin{\alpha}}{\sin{\alpha}-5\cos{\alpha}}\) jest równa:
A. \(-\frac{11}{23}\)
B. \(\frac{24}{5}\)
C. \(-\frac{23}{11}\)
D. \(\frac{5}{24}\)

Zadanie nr 12 — maturalne.
Kąt \(\alpha\) jest ostry i spełnia warunek \(\frac{2\sin{\alpha}+3\cos{\alpha}}{\cos{\alpha}}=4\). Oblicz tangens kąta \(\alpha\).

Zadanie nr 13 — maturalne.
Różnica \(\cos^2{165°} − \sin^2{165°}\) jest równa
A. \(-1\)
B. \(-\frac{3}{2}\)
C. \(-\frac{1}{2}\)
D. \(\frac{\sqrt{3}}{2}\)

Zadanie nr 14 — maturalne.
Kąt \(\alpha\) jest ostry i \(tg{\alpha}=2\). Oblicz wartość wyrażenia \(\sin{2\alpha}\).

Zadanie nr 15 — maturalne.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. Dla każdego kąta ostrego \(\alpha\) wyrażenie \(\sin^4{\alpha}+\sin^2{\alpha}\cdot \cos^2{\alpha}\) jest równe:
A. \(\sin^2{\alpha}\)
B. \(\sin^6{\alpha}\cdot \cos^2{\alpha}\)
C. \(\sin^4{\alpha}+1\)
D. \(\sin^2{\alpha}\cdot (\sin{\alpha}+\cos{\alpha})\cdot (\sin{\alpha}-\cos{\alpha})\)

Zadanie nr 16.
Znaleźć okres podstawowy funkcji: \(y=\cos^4{x}-\sin^4{x}\).
Powiązane materiały
 Tożsamości trygonometryczne
Tożsamości trygonometryczne© medianauka.pl, 2011-03-27, A-1267
Data aktualizacji artykułu: 2023-07-22

 Sinus cosinus tangens cotangens 0 30 45 60 90 stopni
Sinus cosinus tangens cotangens 0 30 45 60 90 stopni Nauka wartości funkcji trygonometrycznych
Nauka wartości funkcji trygonometrycznych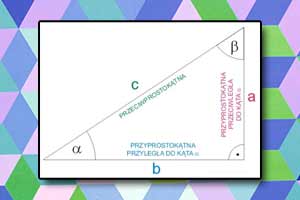 Funkcje trygonometryczne sinus cosinus tangens
Funkcje trygonometryczne sinus cosinus tangens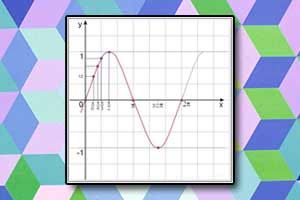 Wykres funkcji sinus
Wykres funkcji sinus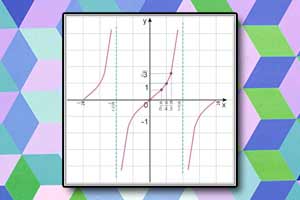 Wykres funkcji tangens
Wykres funkcji tangens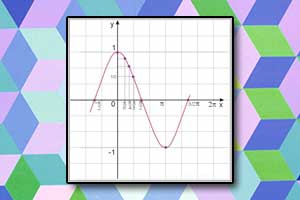 Wykres funkcji cosinus
Wykres funkcji cosinus Wykres funkcji cotangens
Wykres funkcji cotangens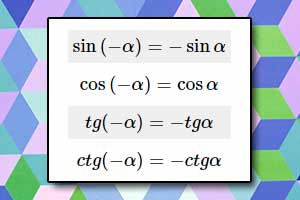 Wzory redukcyjne
Wzory redukcyjne Twierdzenie sinusów, cosinusów i tangensów
Twierdzenie sinusów, cosinusów i tangensów Funkcje cyklometryczne
Funkcje cyklometryczne