Wykres funkcji sinus
Wykresem funkcji sinus jest krzywa, którą nazywamy sinusoidą. Aby sporządzić sinusoidę w układzie kartezjańskim, skorzystamy z pewnych właściwości funkcji sinus.
- Rozpatrujemy tutaj funkcję sinus jako funkcję zmiennej rzeczywistej.
- Okresem podstawowym funkcji sinus jest \(T=2\pi\), tzn. że funkcja przybiera w odstępie co \(T\) te same wartości (jest powtarzalna): \(\sin(x+2\pi)=\sin{x}\).
- Maksymalna wartość funkcji to \(1\), minimalna to \(-1\).
- Przy sporządzaniu wykresu pamiętamy o tabeli:
\(\alpha\) \(0\) \(\frac{\pi}{6}\) \(\frac{\pi}{4}\) \(\frac{\pi}{3}\) \(\frac{\pi}{2}\) \(\sin{\alpha}\) \(0\) \(\frac{1}{2}\) \(\frac{\sqrt{2}}{2}\) \(\frac{\sqrt{3}}{2}\) \(1\) \(\cos{\alpha}\) \(1\) \(\frac{\sqrt{3}}{2}\) \(\frac{\sqrt{2}}{2}\) \(\frac{1}{2}\) \(0\) - Korzystamy także ze wzorów redukcyjnych, aby wyznaczyć wartości funkcji większe od tych zawartych w powyższej tabeli:
\(\sin{(\frac{\pi}{2}+x)}=\cos{x}\)
\(\sin{(\pi+x)}=-\sin{x}\)
Sporządzamy wykres funkcji:
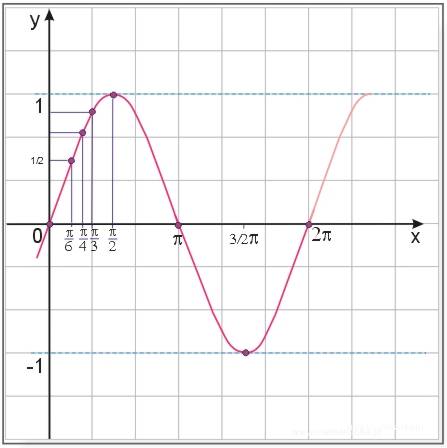
Własności funkcji \(y=\sin{x}\)
- Dziedziną funkcji \(y=\sin{x}\) jest zbiór liczb rzeczywistych.
- Przeciwdziedziną funkcji \(y=\sin{x}\) jest przedział \([-1,1]\).
- Okresem podstawowym funkcji jest \(2\pi\).
- Jest to funkcja nieparzysta.
- Miejsca zerowe funkcji: \(x_0=k\pi,\ k\in \mathbb{Z}\).
Symulacja
Poniższa aplikacja pozwala prześledzić zachowanie się wykresu funkcji sinus w zależności od różnych współczynników.
Funkcja w postaci y = Asin(bx+φ), czyli y = sin(x)
A 1b 1
φ 0
Zadania z rozwiązaniami
Zadanie nr 2.
Znaleźć okres podstawowy funkcji
a) \(y=\sin{2x}\)
b) \(y= \sin{\pi x}\)
Zadanie nr 3 — maturalne.
Na rysunku przedstawiono fragment wykresu funkcji \(f\) określonej dla każdej liczby rzeczywistej \(x\).
Jeden spośród podanych poniżej wzorów jest wzorem tej funkcji. Wskaż wzór funkcji \(f\).
A. \(f(x)=\frac{\cos{x}+1}{|\cos{|x|}+1}\)
B. \(f(x)=\frac{\sin{x}+1}{|\sin{|x|}+1}\)
C. \(f(x)=\frac{\cos{x}-2}{|\cos{|x|}-2}\)
D. \(f(x)=\frac{\sin{x}-2}{|\sin{|x|}-2}\)
Zadanie nr 4 — maturalne.
Jeżeli \(\cos{\beta}=−\frac{1}{3}\) i \(\beta \in (\pi,\frac{3}{2}\pi)\), to wartość wyrażenia \(\sin(\beta−\frac{1}{3}\pi)\) jest równa
A. \(\frac{-2\sqrt{2}+\sqrt{3}}{6}\)
B. \(\frac{2\sqrt{6}+2}{6}\)
C. \(\frac{2\sqrt{2}+\sqrt{3}}{6}\)
D. \(\frac{1-2\sqrt{6}}{6}\)
Inne zagadnienia z tej lekcji
Sinus cosinus tangens cotangens 0 30 45 60 90 stopni
Nauka wartości funkcji trygonometrycznych
Funkcje trygonometryczne sinus cosinus tangens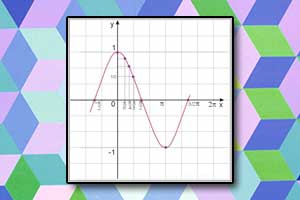
Wykres funkcji cosinus
Wykres funkcji tangens
Wykres funkcji cotangens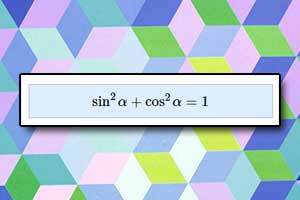
Wzory trygonometryczne, tożsamości trygonometryczne
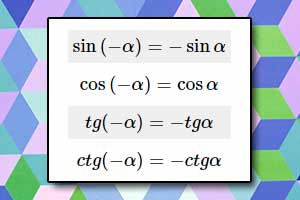Wzory redukcyjne
Twierdzenie sinusów, cosinusów i tangensów
Funkcje cyklometryczne© medianauka.pl, 2011-04-10, A-1293
Data aktualizacji artykułu: 2023-07-21