Nauka » Matematyka » Nierówności trygonometryczne

Zadanie maturalne nr 11, matura 2016 (poziom rozszerzony)

Treść zadania:

Rozwiąż nierówność \(\frac{2cos{x}-\sqrt{3}}{cos^2x}<0\) w przedziale \(\langle 0;2\pi\rangle\).

Rozwiązanie zadania

Określimy najpierw dziedzinę nierówności:

\(\cos^2{x}\neq 0\)

\(\cos{x}\neq 0\\ x\neq \frac{\pi}{2}+2k\pi \vee x\neq -\frac{\pi}{2}+2k\pi\)

W przedziale \(\langle 0;2\pi\rangle\) dziedzina naszej nierówności jest określona następująco:

\(x\neq \frac{\pi}{2}\)

Dalej zauważamy, że mianownik ułamka po lewej stronie nierówności jest dodatni (kwadrat dowolnej liczby jest zawsze dodatni). W takim przypadku aby cały ułamek był ujemny, nasz licznik musi być ujemny.

\(2\cos{x}-\sqrt{3}<0\)

\(2\cos{x}<\sqrt{3}\)

\(\cos{x}<\frac{\sqrt{3}}{2}\)

Dla kąta \(\frac{\pi}{6}\) cosinus przyjmuje wartość równą prawej stronie naszej nierówności elementarnej. Rozwiązanie odczytamy z wykresu.

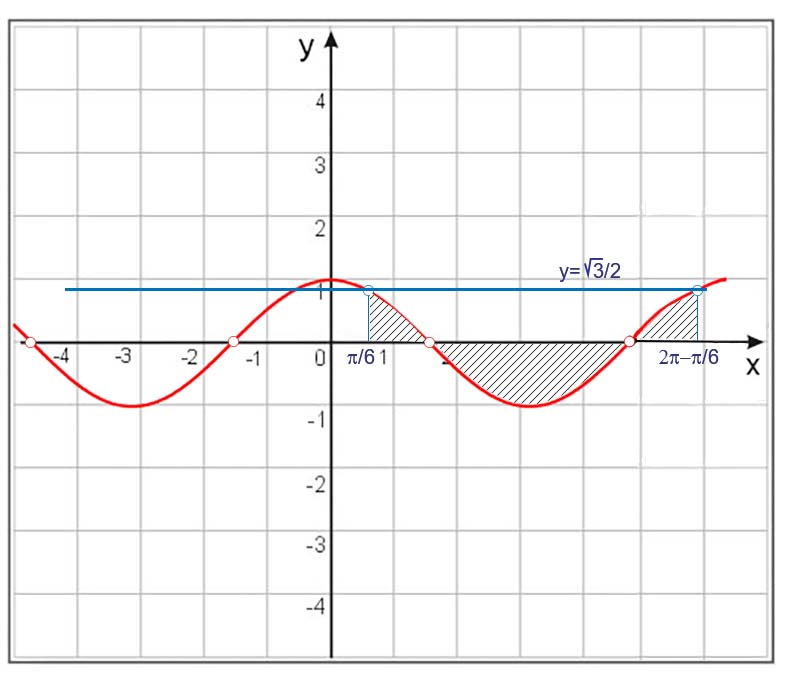
zadanie maturalne nr 11, matura 2016 - ilustracja.

Odpowiedź

\(x\in(\frac{\pi}{6};\frac{\pi}{2})\cup (\frac{\pi}{2};\frac{3\pi}{2})\cup (\frac{3\pi}{2};\frac{11\pi}{6})\)

Matura z matematyki

Zbiór zadań maturalnych z ubiegłych lat na poziomie podstawowym i rozszerzonym oraz centrum dowodzenia dla maturzystów.

Zbiór zadań z matematyki

Zbiór zadań z matematyki wraz z pełnymi rozwiązaniami. W naszej bazie zgromadziliśmy ponad tysiąc zadań.

WYKRESY ONLINE

Narysuj wykres funkcji w programie do szkicowania wykresów i odczytaj jego własności.

Zadania podobne

Zadanie nr 1.

Rozwiązać nierówność:

a) \(tgx\leq \sqrt{3}\)

b) \(2\cos{x}>4\)

Pokaż rozwiązanie zadania.

Zadanie nr 2.

Rozwiązać nierówność:

a) \(\sin{(3x-\frac{\pi}{2})}<\sqrt{2}\)

b) \(ctg3x<1\)

Pokaż rozwiązanie zadania.