Nauka » Matematyka » Pole koła i długość okręgu

Zadanie - obwód koła

Treść zadania:

Ile potrzeba sznurka, aby ułożyć z niego okrąg o średnicy 2 m?

Rozwiązanie zadania

Gdy sznurek układamy w okrąg, to długość sznurka będzie stanowić obwód tego okręgu, który obliczamy ze wzoru:

S = 2 π r

Mamy daną średnicę okręgu, promień ma długość połowy średnicy, więc:

$d = 2 m$

$S = 2 π r = 2 π \cdot \frac{d}{2} = π d = 2 π m \approx 6, 28 m$

Odpowiedź

S \approx 6, 28

Matura z matematyki

Zbiór zadań maturalnych z ubiegłych lat na poziomie podstawowym i rozszerzonym oraz centrum dowodzenia dla maturzystów.

Zbiór zadań z matematyki

Zbiór zadań z matematyki wraz z pełnymi rozwiązaniami. W naszej bazie zgromadziliśmy ponad tysiąc zadań.

WYKRESY ONLINE

Narysuj wykres funkcji w programie do szkicowania wykresów i odczytaj jego własności.

Zadania podobne

Zadanie nr 1.

Obliczyć pole koła o średnicy $d = \sqrt{2}$ .

Pokaż rozwiązanie zadania.

Zadanie nr 2.

Obliczyć długość okręgu o średnicy $d = 7$ .

Pokaż rozwiązanie zadania.

Zadanie nr 3.

Jaki promień ma koło o polu równym 1?

Pokaż rozwiązanie zadania.

Zadanie nr 4.

Pole koła jest równe $π$ . Jaki promień ma koło o polu dwa razy mniejszym? Oblicz stosunek promieni tych okręgów.

Pokaż rozwiązanie zadania.

Zadanie nr 5.

Z kwadratowej blachy o boku długości 1 m wycięto koła o promieniu $r = 10 c m$ tak, że środki tych kół leżą na prostych równoległych i prostopadłych. Jaka jest powierzchnia ścinków? Jaki procent powierzchni blachy stanowią ścinki?

Pokaż rozwiązanie zadania.

Zadanie nr 6.

W koło o promieniu $r$ wpisano kwadrat. Oblicz pole figury, która stanowi różnicę tego koła i kwadratu?

Pokaż rozwiązanie zadania.

Zadanie nr 7.

Na trójkącie równobocznym o boku $a = 1$ opisano okrąg. Oblicz obwód tego okręgu i pole koła wyznaczonego przez ten okrąg.

Pokaż rozwiązanie zadania.

Zadanie nr 8.

W trójkąt równoboczny o boku długości $a = 1$ wpisano koło. Oblicz jego pole i obwód.

Pokaż rozwiązanie zadania.

Zadanie nr 9.

Na trójkącie prostokątnym o przyprostokątnych długości 3 i 4 opisano koło. Oblicz pole i obwód tego koła.

Pokaż rozwiązanie zadania.

Zadanie nr 10.

Oblicz długość okręgu danego równaniem $(x - 1)^{2} + (y - 1)^{2} = 2$ .

Pokaż rozwiązanie zadania.

Zadanie nr 11 — maturalne.

Pole figury $F_{1}$ złożonej z dwóch stycznych zewnętrznie kół o promieniach 1 i 3 jest równe polu figury $F_{2}$ złożonej z dwóch stycznych zewnętrznie kół o promieniach długości $r$ (zobacz rysunek).

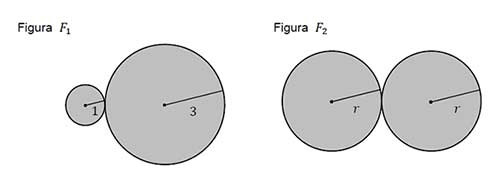
Rysunek do zadani amaturalnego nr 24, 2021

Długość $r$ promienia jest równa

A. $\sqrt{3}$

B. $2$

C. $\sqrt{5}$

D. $3$

Pokaż rozwiązanie zadania.