Pole kwadratu

Jak obliczyć pole powierzchni kwadratu?

Pole kwadratu wyraża się wzorem:

Wielkość \(a\) jest długością boku kwadratu.

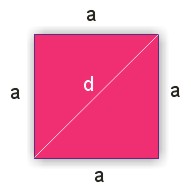
pole kwadratu

Przykład

Obliczyć pole kwadratu o boku długości 10.

Rozwiązanie: Dana jest długość boku kwadratu \(a=10\). Stosujemy więc bezpośrednio wzór na pole kwadratu:

\(P=a^2=10^2=100\)

Wzór na pole z przekątną kwadratu

W przypadku kwadratu jego pole można wyrazić poprzez jego przekątną.

Pole kwadratu w przypadku, gdy dana jest jego przekątna \(d\), wyraża się wzorem:

\(P=\frac{1}{2}d^2\)

Dowód

Przekątna w kwadracie jest wyrażona wzorem \(d=a\sqrt{2}\). Wzór ten wynika z twierdzenia Pitagorasa. Ponieważ mamy do czynienia z długościami, czyli liczbami dodatnimi, można zapisać, że \(d^2=(a\sqrt{2})^2=2a^2\).

Stąd \(a^2=P=\frac{1}{2}d^2\).

Obwód kwadratu

Ponieważ w kwadracie wszystkie boki są równe, obwód jest równy ich łącznej długości.

Obwód kwadratu o boku \(a\) wyraża się wzorem:

\(L=4a\)

Przykład

Jakie jest pole kwadratu o obwodzie 12 cm?

Obwód tego kwadratu wynosi \(L=4a=12 cm\), stąd:

\(4a=12\ cm/:4\)

\( a=3\ cm\)

Pole kwadratu obliczamy następująco:

\(P=a^2=(3\ cm)^2=9\ cm^2\)

Zadania z rozwiązaniami

Zadanie nr 1.

Na kole o promieniu \(r=5\) opisano kwadrat. Oblicz jego pole.

Pokaż rozwiązanie zadania.

Zadanie nr 2.

Oblicz pole kwadratu \(ABCD\), jeżeli wiadomo, że \(A=(3,0), B=(4,2), C=(2,3), D=(1,1)\).

Pokaż rozwiązanie zadania.

Zadanie nr 3.

Na obszarze w kształcie kwadratu o powierzchni 1 ha organizowany jest koncert. Przyjmuje się, że na dany obszar można wpuścić tyle ludzi, że na każdego przypada 1 m² wolnej powierzchni. Jaki przychód z koncertu będą mieli organizatorzy, jeśli zostaną sprzedane wszystkie bilety, których cena wynosi 30 zł?

Pokaż rozwiązanie zadania.

Zadanie nr 4.

Środki kwadratu o boku \(a=10\) połączono tak, że powstał w środku mniejszy kwadrat. Oblicz jego pole.

Pokaż rozwiązanie zadania.

Zadanie nr 5.

Przekątna kwadratu pokrywa się z ramieniem trójkąta równoramiennego o polu równym 16. Oblicz pole kwadratu.

Pokaż rozwiązanie zadania.

Zadanie nr 6 — maturalne.

Dany jest kwadrat \(ABCD\), w którym \(A=(5, -\frac{5}{3})\). Przekątna \(BD\) tego kwadratu jest zawarta w prostej o równaniu \(y =\frac{4}{3}x\). Oblicz współrzędne punktu przecięcia przekątnych \(AC\) i \(BD\) oraz pole kwadratu \(ABCD\).

Pokaż rozwiązanie zadania.

Zadanie nr 7 — maturalne.

Punkt \(A=(3,−5)\) jest wierzchołkiem kwadratu \(ABCD\), a punkt \(M=(1,3)\) jest punktem przecięcia się przekątnych tego kwadratu. Wynika stąd, że pole kwadratu \(ABCD\) jest równe

A. \(68\)

B. \(136\)

C. \(2\sqrt{34}\)

D. \(8\sqrt{34}\)

Pokaż rozwiązanie zadania.