Pole trójkąta
Istnieje co najmniej kilka wzorów na pole trójkąta. Ich stosowanie zależy od posiadanych danych i czasem od rodzaju trójkąta, z jakim mamy do czynienia.
Poniżej przedstawiony został podstawowy wzór na pole trójkąta:
Wzór na pole trójkąta wyraża się wzorem:
Wielkość \(h\) jest wysokością trójkąta, natomiast \(a\) jest długością podstawy trójkąta, na którą została opuszczona wysokość.
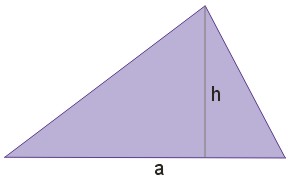
Przykład
Obliczyć pole trójkąta przedstawionego na rysunku.
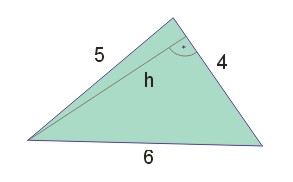
Rozwiązanie: Dana jest wysokość \(h\), opuszczona na bok trójkąta o długości 4. Stosujemy więc wzór na pole trójkąta:
\(P=\frac{1}{2}\cdot 4\cdot h=2h\)
Inne wzory na pole trójkąta
Pole trójkąta wyraża się wzorem:
gdzie \(a, b\) są długościami boków trójkąta, a \(\gamma\) jest kątem między tymi bokami.
Przykład
Jakie pole ma trójkąt przedstawiony na rysunku.
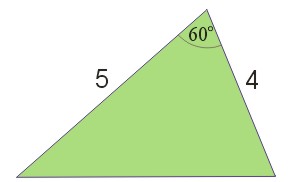
Rozwiązanie: Mamy dane dwie długości boków i kąt między nimi. Możemy więc zastosować powyższy wzór. Sinus kąta 60° jest równy \(\frac{\sqrt{3}}{2}\). Mamy więc:
\(P=\frac{1}{2}ab\sin{\gamma}=\frac{1}{2}\cdot 4 \cdot 5 \cdot \sin{60^o}=10\cdot \frac{\sqrt{3}}{2}=5\sqrt{3}\)
Wzór Herona
Gdy dane są długości trzech boków trójkąta, wzór na pole powierzchni trójkąta przyjmuje następującą postać:
Wielkości a, b, c są długościami boków trójkąta.
Pole trójkąta wpisanego i opisanego na okręgu
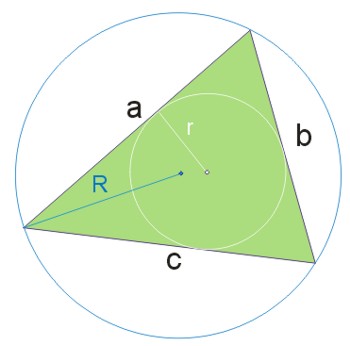
Pole trójkąta, na którym opisano okrąg, wyraża się wzorem:
Wielkości \(a, b, c\) są długościami boków trójkąta, \(R\) — długością promienia okręgu opisanego na trójkącie.
Pole trójkąta, w który wpisano okrąg, wyraża się wzorem:
Wielkości \(a, b, c\) są długościami boków trójkąta, \(r\) — długością promienia okręgu wpisanego w trójkąt.
Pole trójkąta wyznaczonego przez dwa wektory
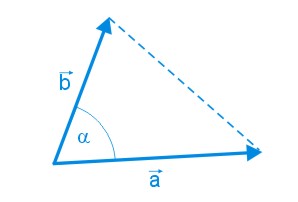
Pole trójkąta wyznaczonego przez dwa niezerowe wektory zaczepione we wspólnym początku jest równe połowie modułu wyznacznika tych wektorów.
\(W=\begin{vmatrix} a_x&a_y\\b_x&b_y \end{vmatrix}=a_xb_y-a_yb_x\)
\( P=\frac{1}{2}|W|\)
Przykłady
Wyznaczyć pole trójkąta wyznaczonego przez wektory \([-1,1] i [4,3]\).
Korzystamy z powyższego twierdzenia i obliczamy wyznacznik wektorów:
\(W=\begin{vmatrix} -1&1\\4&3 \end{vmatrix}=(-1)\cdot 3-1\cdot 4=-3-4=-7\)
\(P=\frac{1}{2}\cdot |-7|=3\frac{1}{2}\)
Pole trójkąta, gdy dane są współrzędne wierzchołków
Pole trójkąta o wierzchołkach \(P_1(x_1,y_1), \ P_2(x_2,y_2), \ P_3(x_3,y_3)\) wyraża się wzorem:
Pole trójkąta równobocznego
Możemy wyrazić pole powierzchni trójkąta równobocznego tylko w zależności od długości jego boku.
\(P=\frac{1}{2}ah=\frac{1}{2}a\cdot \frac{1}{2}a\sqrt{3}=\frac{a^2\sqrt{3}}{4}\)
Zatem pole powierzchni trójkąta równobocznego wyraża się wzorem:
\(P=\frac{a^2\sqrt{3}}{4}\)
Pole trójkąta równobocznego
Pole powierzchni dowolnego trójkąta wyraża się wzorem: \(P=\frac{1}{2}ah\), gdzie \(a\) jest długością boku trójkąta, a \(h\) jego wysokością. Ponieważ wyżej wyznaczyliśmy wysokość trójkąta, możemy wyrazić pole powierzchni trójkąta równobocznego tylko w zależności od długości jego boku.
\(P=\frac{1}{2}ah=\frac{1}{2}a\cdot \frac{1}{2}a\sqrt{3}=\frac{a^2\sqrt{3}}{4}\)
Zatem wzór na pole powierzchni trójkąta równobocznego jest następujący:
Przykład
Jakie pole ma trójkąt równoboczny o obwodzie 12?
Jeżeli obwód \(L=12\), to bok trójkąta równobocznego ma długość \(a=\frac{12}{3}=4\).
Zatem pole \(P=\frac{a^2\sqrt{3}}{4}=4\sqrt{3}\).
Obwód trójkąta
Obwód trójkąta wyraża się wzorem:
Wielkości \(a, b, c\) są długościami boków trójkąta.
Obwód trójkąta równobocznego o boku \(a\) wyraża się wzorem:
Wielkości \(a, b, c\) są długościami boków trójkąta.
Pytania
Jak obliczyć pole trójkąta prostokątnego?
W przypadku trójkąta prostokątnego jego wysokość jest jednocześnie jego przyprostokątną. Zatem pole powierzchni trójkąta prostokątnego o przyprostokątnych \(a\) i \(b\) jego pole obliczymy ze wzoru \(P=\frac{ab}{2}\).
Zadania z rozwiązaniami
Zadanie nr 1.
Z kwadratu o boku a wycięto trójkąt tak, że jeden z jego wierzchołków stanowi środek boku kwadratu, a jeden z boków tego trójkąta stanowi bok kwadratu. Czy pole ścinków jest większe od pola trójkąta?
Zadanie nr 2 — maturalne.
Dany jest trójkąt równoboczny \(ABC\). Na bokach \(AB\) i \(AC\) wybrano punkty — odpowiednio — \(D\) i \(E\) takie, że \(|BD|=|AE=\frac{1}{3}|AB|\). Odcinki \(CD\) i \(BE\) przecinają się w punkcie \(P\) (zobacz rysunek).
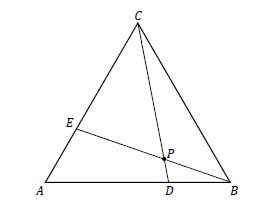
Wykaż, że pole trójkąta \(DBP\) jest 21 razy mniejsze od pola trójkąta \(ABC\).
Zadanie nr 3 — maturalne.
Punkty \(A=(−20, 12)\) i \(B=(7, 3)\) są wierzchołkami trójkąta równoramiennego ABC, w którym \(|AC|=|BC|\). Wierzchołek \(C\) leży na osi \(Oy\) układu współrzędnych. Oblicz współrzędne wierzchołka \(C\) oraz obwód tego trójkąta.
Zadanie nr 4 — maturalne.
Przyprostokątna \(AC\) trójkąta prostokątnego ABC ma długość 8 oraz \(tg\alpha=\frac{2}{5}\) (zobacz rysunek).
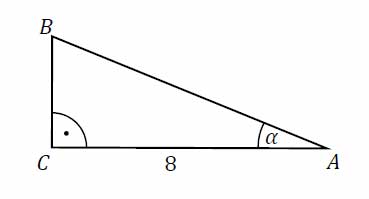
Pole tego trójkąta jest równe
A. \(12\)
B. \(\frac{37}{3}\)
C. \(\frac{62}{5}\)
D. \(\frac{64}{5}\)
Zadanie nr 5 — maturalne.
W trójkącie równoramiennym wysokość opuszczona na podstawę jest równa 36, a promień okręgu wpisanego w ten trójkąt jest równy 10. Oblicz długości boków tego trójkąta i promień okręgu opisanego na tym trójkącie.
Zadanie nr 6 — maturalne.
W trójkącie ostrokątnym \(ABC\) bok \(AB\) ma długość \(c\), długość boku \(BC\) jest równa a oraz \(\angle ABC=\beta\). Dwusieczna kąta \(ABC\) przecina bok \(AC\) trójkąta w punkcie \(E\). Wykaż, że długość odcinka \(BE\) jest równa \(\frac{2ac\cdot \cos{\frac{\beta}{2}}}{a+c}\).
Zadanie nr 7 — maturalne.
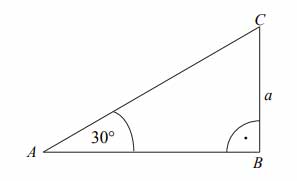
Obwód trójkąta \(ABC\), przedstawionego na rysunku, jest równy:
A. \(3+\frac{\sqrt{3}}{2}\)
B. \(2+\frac{\sqrt{2}}{2}\)
C. \(3+\sqrt{3}\)
D. \((2+\sqrt{2}\)
Zadanie nr 8 — maturalne.
Kąt \(CAB\) trójkąta prostokątnego \(ACB\) ma miarę \(30°\). Pole kwadratu \(DEFG\), wpisanego w ten trójkąt (zobacz rysunek), jest równe 4. Oblicz pole trójkąta \(ACB\).
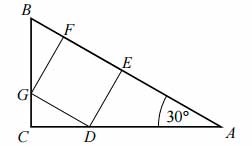
Zadanie nr 9 — maturalne.
Okręgi o promieniach 3 i 4 są styczne zewnętrznie. Prosta styczna do okręgu o promieniu 4 w punkcie \(P\) przechodzi przez środek okręgu o promieniu 3 (zobacz rysunek).
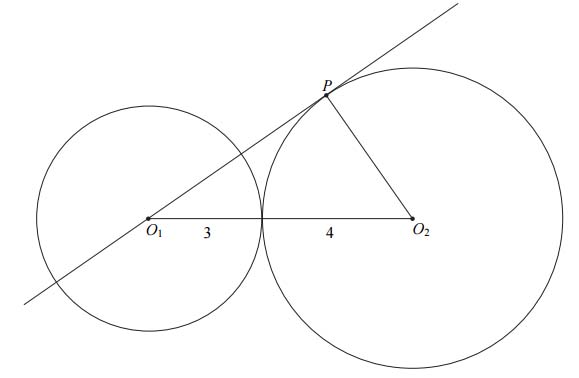
Pole trójkąta, którego wierzchołkami są środki okręgów i punkt styczności \(P\), jest równe:
A. \(14\)
B. \(2\sqrt{33}\)
C. \(4\sqrt{33}\)
D. \(12\)
Zadanie nr 10.
W trójkąt równoramienny o polu \(\sqrt{15}\) wpisano okrąg o promieniu \(r=\frac{\sqrt{15}}{5}\). Na tym samy trójkącie opisano okrąg o promieniu \(R=\frac{8\sqrt{15}}{15}\). Oblicz długości boków tego trójkąta.
Zadanie nr 11.
Obliczyć pole i obwód trójkąta prostokątnego, wyznaczonego przez punkty \(A=(1,2), B=(1,3), C=(4,1)\).
Zadanie nr 12.
Dany jest trójkąt \(A, B, C\) o wierzchołkach \(A=(-1,1), B=(2,1), C=(-2,-1)\). Oblicz jego pole.
Zadanie nr 13.
Na trójkącie o polu równym 6 i o bokach o długości 2, 3 i 4 opisano okrąg. Oblicz długość promienia tego okręgu.
Zadanie nr 14.
Dany jest trójkąt równoramienny o ramionach długości 5 i kącie wewnętrznym między tymi ramionami \(\alpha=30°\). Oblicz pole powierzchni tego trójkąta.
Zadanie nr 15.
Dany jest wektor \(\vec{AB}=[2,5]\) zaczepiony w punkcie \(A=(1,1)\). Znaleźć taki punkt \(C\), leżący na prostej \(y=2\), że pole trójkąta \(ABC\) jest równe 10.
Zadanie nr 16.
Wektory \(\vec{a}=[1,2], \vec{b}=[-3,4]\) wyznaczają trójkąt. Obliczyć jego pole.
Zadanie nr 17.
Dany jest trójkąt o bokach długości 2, 3 i 4. Oblicz pole powierzchni tego trójkąta.
Zadanie nr 18.
Ceny poszczególnych działek są następujące:
A. 60 000 PLN
B. 50 000 PLN
C. 50 000 PLN
D. 100 000 PLN
Zakup której działki jest najbardziej opłacalny?
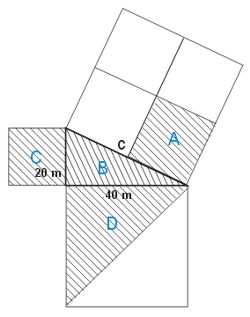
Zadanie nr 19.
Środki trójkąta równobocznego o boku długości 2 połączono ze sobą tak, że powstał mniejszy trójkąt wewnątrz większego. Obliczyć jego pole.
Zadanie nr 20.
Oblicz pole powierzchni i obwód trójkąta równobocznego o wysokości \(h=2 cm\).
Wybrane karty pracy
Pole trójkąta
Powiązane materiały
Twierdzenie Pitagorasa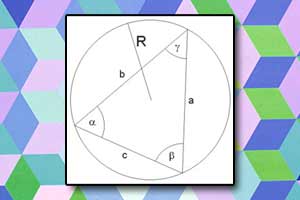
Twierdzenie sinusów, cosinusów i tangensów
Twierdzenia o trójkącie, pole trójkąta
Trójkąt równoboczny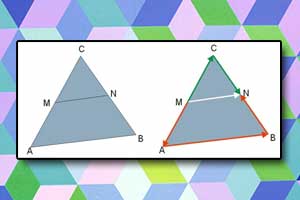
Twierdzenia o trójkącie
Trójkąt
Pole powierzchni trójkąta
Pole jako wyrażenie — quiz
Pole trójkąta — quiz© medianauka.pl, 2010-12-18, A-1056
Data aktualizacji artykułu: 2023-06-17